Deep Dependency Networks and Advanced Inference Schemes for Multi-Label Classification

We present a unified framework called deep dependency networks (DDNs) that combines dependency networks and deep learning architectures for multi-label classification, with a particular emphasis on image and video data. The primary advantage of dependency networks is their ease of training, in contrast to other probabilistic graphical models like Markov networks. In particular, when combined with deep learning architectures, they provide an intuitive, easy-to-use loss function for multi-label classification. A drawback of DDNs compared to Markov networks is their lack of advanced inference schemes, necessitating the use of Gibbs sampling. To address this challenge, we propose novel inference schemes based on local search and integer linear programming for computing the most likely assignment to the labels given observations. We evaluate our novel methods on three video datasets (Charades, TACoS, Wetlab) and three image datasets (MS-COCO, PASCAL VOC, NUS-WIDE), comparing their performance with (a) basic neural architectures and (b) neural architectures combined with Markov networks equipped with advanced inference and learning techniques. Our results demonstrate the superiority of our new DDN methods over the two competing approaches.

Learning to Solve the Constrained Most Probable Explanation Task in Probabilistic Graphical Models

We propose a self-supervised learning approach for solving the following constrained optimization task in log-linear models or Markov networks. Let $f$ and $g$ be two log-linear models defined over the sets $\mathbf{X}$ and $\mathbf{Y}$ of random variables respectively. Given an assignment $\mathbf{x}$ to all variables in $\mathbf{X}$ (evidence) and a real number $q$, the constrained most-probable explanation (CMPE) task seeks to find an assignment $\mathbf{y}$ to all variables in $\mathbf{Y}$ such that $f(\mathbf{x}, \mathbf{y})$ is maximized and $g(\mathbf{x}, \mathbf{y})\leq q$. In our proposed self-supervised approach, given assignments $\mathbf{x}$ to $\mathbf{X}$ (data), we train a deep neural network that learns to output near-optimal solutions to the CMPE problem without requiring access to any pre-computed solutions. The key idea in our approach is to use first principles and approximate inference methods for CMPE to derive novel loss functions that seek to push infeasible solutions towards feasible ones and feasible solutions towards optimal ones. We analyze the properties of our proposed method and experimentally demonstrate its efficacy on several benchmark problems.

Neural Network Approximators for Marginal MAP in Probabilistic Circuits

Probabilistic circuits (PCs) such as sum-product networks efficiently represent large multi-variate probability distributions. They are preferred in practice over other probabilistic representations such as Bayesian and Markov networks because PCs can solve marginal inference (MAR) tasks in time that scales linearly in the size of the network. Unfortunately, the maximum-a-posteriori (MAP) and marginal MAP (MMAP) tasks remain NP-hard in these models. Inspired by the recent work on using neural networks for generating near-optimal solutions to optimization problems such as integer linear programming, we propose an approach that uses neural networks to approximate (M)MAP inference in PCs. The key idea in our approach is to approximate the cost of an assignment to the query variables using a continuous multilinear function, and then use the latter as a loss function. The two main benefits of our new method are that it is self-supervised and after the neural network is learned, it requires only linear time to output a solution. We evaluate our new approach on several benchmark datasets and show that it outperforms three competing linear time approximations, max-product inference, max-marginal inference and sequential estimation, which are used in practice to solve MMAP tasks in PCs.

CaptainCook4D: A dataset for understanding errors in procedural activities

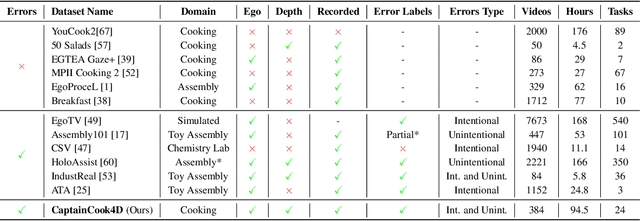
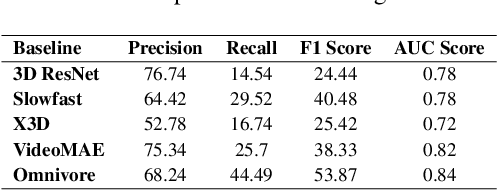
Following step-by-step procedures is an essential component of various activities carried out by individuals in their daily lives. These procedures serve as a guiding framework that helps to achieve goals efficiently, whether it is assembling furniture or preparing a recipe. However, the complexity and duration of procedural activities inherently increase the likelihood of making errors. Understanding such procedural activities from a sequence of frames is a challenging task that demands an accurate interpretation of visual information and the ability to reason about the structure of the activity. To this end, we collect a new egocentric 4D dataset, CaptainCook4D, comprising 384 recordings (94.5 hours) of people performing recipes in real kitchen environments. This dataset consists of two distinct types of activity: one in which participants adhere to the provided recipe instructions and another in which they deviate and induce errors. We provide 5.3K step annotations and 10K fine-grained action annotations and benchmark the dataset for the following tasks: supervised error recognition, multistep localization, and procedure learning

Deep Dependency Networks for Multi-Label Classification

We propose a simple approach which combines the strengths of probabilistic graphical models and deep learning architectures for solving the multi-label classification task, focusing specifically on image and video data. First, we show that the performance of previous approaches that combine Markov Random Fields with neural networks can be modestly improved by leveraging more powerful methods such as iterative join graph propagation, integer linear programming, and $\ell_1$ regularization-based structure learning. Then we propose a new modeling framework called deep dependency networks, which augments a dependency network, a model that is easy to train and learns more accurate dependencies but is limited to Gibbs sampling for inference, to the output layer of a neural network. We show that despite its simplicity, jointly learning this new architecture yields significant improvements in performance over the baseline neural network. In particular, our experimental evaluation on three video activity classification datasets: Charades, Textually Annotated Cooking Scenes (TACoS), and Wetlab, and three multi-label image classification datasets: MS-COCO, PASCAL VOC, and NUS-WIDE show that deep dependency networks are almost always superior to pure neural architectures that do not use dependency networks.