Learning to Guide Local Search for MPE Inference in Probabilistic Graphical Models

Most Probable Explanation (MPE) inference in Probabilistic Graphical Models (PGMs) is a fundamental yet computationally challenging problem arising in domains such as diagnosis, planning, and structured prediction. In many practical settings, the graphical model remains fixed while inference must be performed repeatedly for varying evidence patterns. Stochastic Local Search (SLS) algorithms scale to large models but rely on myopic best-improvement rule that prioritizes immediate likelihood gains and often stagnate in poor local optima. Heuristics such as Guided Local Search (GLS+) partially alleviate this limitation by modifying the search landscape, but their guidance cannot be reused effectively across multiple inference queries on the same model. We propose a neural amortization framework for improving local search in this repeated-query regime. Exploiting the fixed graph structure, we train an attention-based network to score local moves by predicting their ability to reduce Hamming distance to a near-optimal solution. Our approach integrates seamlessly with existing local search procedures, using this signal to balance short-term likelihood gains with long-term promise during neighbor selection. We provide theoretical intuition linking distance-reducing move selection to improved convergence behavior, and empirically demonstrate consistent improvements over SLS and GLS+ on challenging high-treewidth benchmarks in the amortized inference setting.

Learning to Solve the Constrained Most Probable Explanation Task in Probabilistic Graphical Models

We propose a self-supervised learning approach for solving the following constrained optimization task in log-linear models or Markov networks. Let $f$ and $g$ be two log-linear models defined over the sets $\mathbf{X}$ and $\mathbf{Y}$ of random variables respectively. Given an assignment $\mathbf{x}$ to all variables in $\mathbf{X}$ (evidence) and a real number $q$, the constrained most-probable explanation (CMPE) task seeks to find an assignment $\mathbf{y}$ to all variables in $\mathbf{Y}$ such that $f(\mathbf{x}, \mathbf{y})$ is maximized and $g(\mathbf{x}, \mathbf{y})\leq q$. In our proposed self-supervised approach, given assignments $\mathbf{x}$ to $\mathbf{X}$ (data), we train a deep neural network that learns to output near-optimal solutions to the CMPE problem without requiring access to any pre-computed solutions. The key idea in our approach is to use first principles and approximate inference methods for CMPE to derive novel loss functions that seek to push infeasible solutions towards feasible ones and feasible solutions towards optimal ones. We analyze the properties of our proposed method and experimentally demonstrate its efficacy on several benchmark problems.

Neural Network Approximators for Marginal MAP in Probabilistic Circuits

Probabilistic circuits (PCs) such as sum-product networks efficiently represent large multi-variate probability distributions. They are preferred in practice over other probabilistic representations such as Bayesian and Markov networks because PCs can solve marginal inference (MAR) tasks in time that scales linearly in the size of the network. Unfortunately, the maximum-a-posteriori (MAP) and marginal MAP (MMAP) tasks remain NP-hard in these models. Inspired by the recent work on using neural networks for generating near-optimal solutions to optimization problems such as integer linear programming, we propose an approach that uses neural networks to approximate (M)MAP inference in PCs. The key idea in our approach is to approximate the cost of an assignment to the query variables using a continuous multilinear function, and then use the latter as a loss function. The two main benefits of our new method are that it is self-supervised and after the neural network is learned, it requires only linear time to output a solution. We evaluate our new approach on several benchmark datasets and show that it outperforms three competing linear time approximations, max-product inference, max-marginal inference and sequential estimation, which are used in practice to solve MMAP tasks in PCs.

Don't Explain without Verifying Veracity: An Evaluation of Explainable AI with Video Activity Recognition

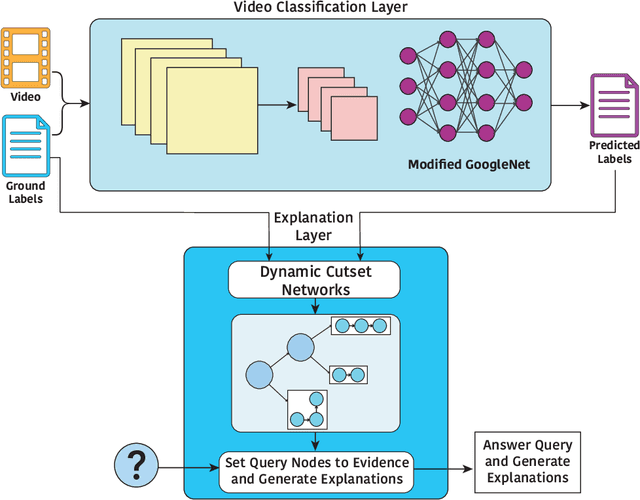
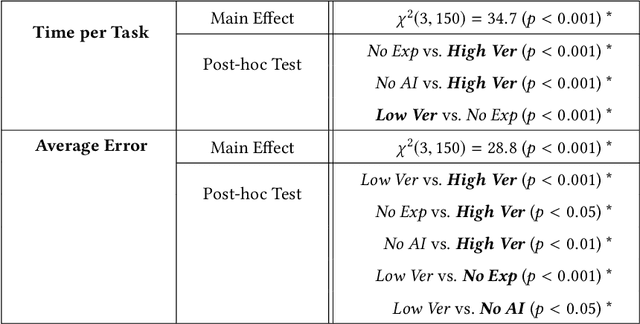
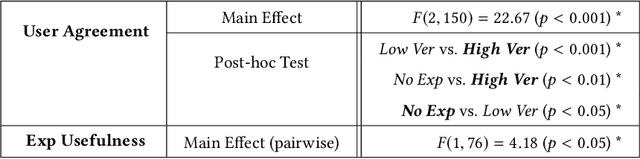
Explainable machine learning and artificial intelligence models have been used to justify a model's decision-making process. This added transparency aims to help improve user performance and understanding of the underlying model. However, in practice, explainable systems face many open questions and challenges. Specifically, designers might reduce the complexity of deep learning models in order to provide interpretability. The explanations generated by these simplified models, however, might not accurately justify and be truthful to the model. This can further add confusion to the users as they might not find the explanations meaningful with respect to the model predictions. Understanding how these explanations affect user behavior is an ongoing challenge. In this paper, we explore how explanation veracity affects user performance and agreement in intelligent systems. Through a controlled user study with an explainable activity recognition system, we compare variations in explanation veracity for a video review and querying task. The results suggest that low veracity explanations significantly decrease user performance and agreement compared to both accurate explanations and a system without explanations. These findings demonstrate the importance of accurate and understandable explanations and caution that poor explanations can sometimes be worse than no explanations with respect to their effect on user performance and reliance on an AI system.