Effectiveness of Function Matching in Driving Scene Recognition

Knowledge distillation is an effective approach for training compact recognizers required in autonomous driving. Recent studies on image classification have shown that matching student and teacher on a wide range of data points is critical for improving performance in distillation. This concept (called function matching) is suitable for driving scene recognition, where generally an almost infinite amount of unlabeled data are available. In this study, we experimentally investigate the impact of using such a large amount of unlabeled data for distillation on the performance of student models in structured prediction tasks for autonomous driving. Through extensive experiments, we demonstrate that the performance of the compact student model can be improved dramatically and even match the performance of the large-scale teacher by knowledge distillation with massive unlabeled data.

Feature Space Particle Inference for Neural Network Ensembles

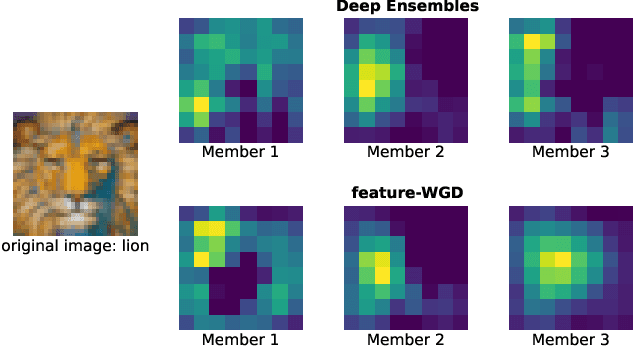
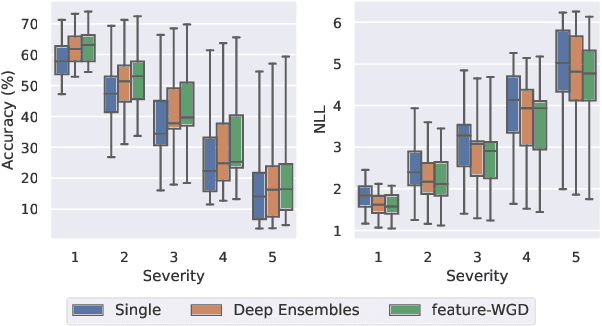
Ensembles of deep neural networks demonstrate improved performance over single models. For enhancing the diversity of ensemble members while keeping their performance, particle-based inference methods offer a promising approach from a Bayesian perspective. However, the best way to apply these methods to neural networks is still unclear: seeking samples from the weight-space posterior suffers from inefficiency due to the over-parameterization issues, while seeking samples directly from the function-space posterior often results in serious underfitting. In this study, we propose optimizing particles in the feature space where the activation of a specific intermediate layer lies to address the above-mentioned difficulties. Our method encourages each member to capture distinct features, which is expected to improve ensemble prediction robustness. Extensive evaluation on real-world datasets shows that our model significantly outperforms the gold-standard Deep Ensembles on various metrics, including accuracy, calibration, and robustness. Code is available at https://github.com/DensoITLab/featurePI .

Exponential Convergence Rates of Classification Errors on Learning with SGD and Random Features

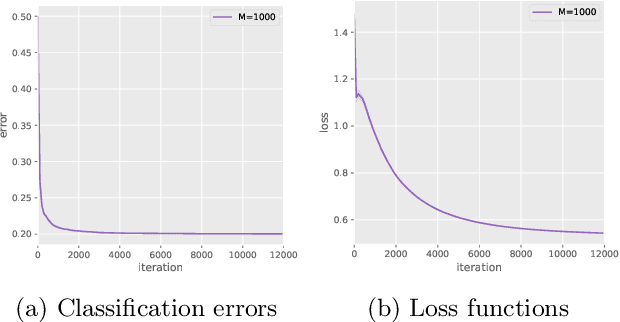
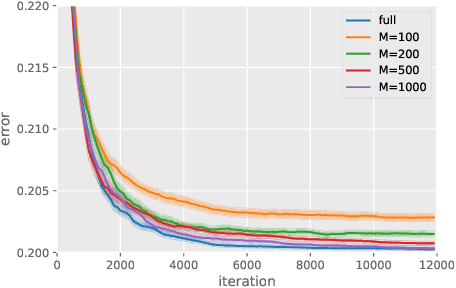
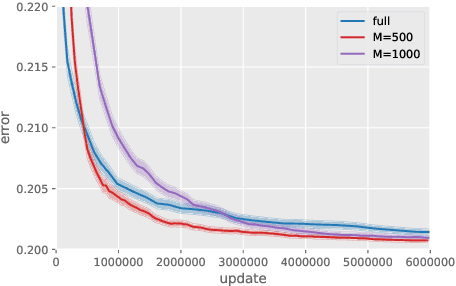
Although kernel methods are widely used in many learning problems, they have poor scalability to large datasets. To address this problem, sketching and stochastic gradient methods are the most commonly used techniques to derive efficient large-scale learning algorithms. In this study, we consider solving a binary classification problem using random features and stochastic gradient descent. In recent research, an exponential convergence rate of the expected classification error under the strong low-noise condition has been shown. We extend these analyses to a random features setting, analyzing the error induced by the approximation of random features in terms of the distance between the generated hypothesis including population risk minimizers and empirical risk minimizers when using general Lipschitz loss functions, to show that an exponential convergence of the expected classification error is achieved even if random features approximation is applied. Additionally, we demonstrate that the convergence rate does not depend on the number of features and there is a significant computational benefit in using random features in classification problems because of the strong low-noise condition.