Unsupervised Video Interpolation by Learning Multilayered 2.5D Motion Fields

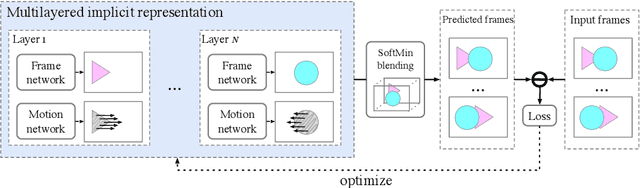
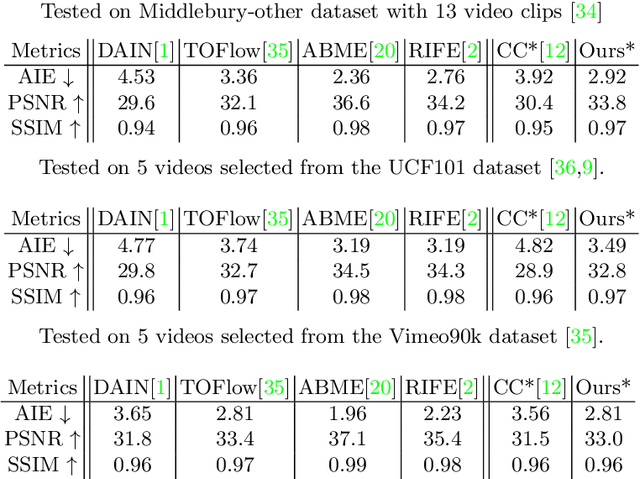
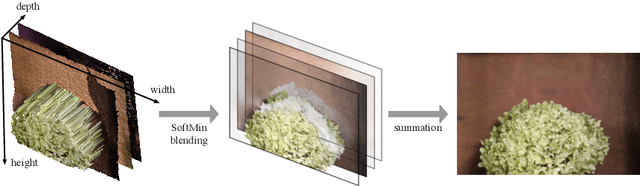
The problem of video frame interpolation is to increase the temporal resolution of a low frame-rate video, by interpolating novel frames between existing temporally sparse frames. This paper presents a self-supervised approach to video frame interpolation that requires only a single video. We pose the video as a set of layers. Each layer is parameterized by two implicit neural networks -- one for learning a static frame and the other for a time-varying motion field corresponding to video dynamics. Together they represent an occlusion-free subset of the scene with a pseudo-depth channel. To model inter-layer occlusions, all layers are lifted to the 2.5D space so that the frontal layer occludes distant layers. This is done by assigning each layer a depth channel, which we call `pseudo-depth', whose partial order defines the occlusion between layers. The pseudo-depths are converted to visibility values through a fully differentiable SoftMin function so that closer layers are more visible than layers in a distance. On the other hand, we parameterize the video motions by solving an ordinary differentiable equation (ODE) defined on a time-varying neural velocity field that guarantees valid motions. This implicit neural representation learns the video as a space-time continuum, allowing frame interpolation at any temporal resolution. We demonstrate the effectiveness of our method on real-world datasets, where our method achieves comparable performance to state-of-the-arts that require ground truth labels for training.

Learning to Estimate Hidden Motions with Global Motion Aggregation

Occlusions pose a significant challenge to optical flow algorithms that rely on local evidences. We consider an occluded point to be one that is imaged in the first frame but not in the next, a slight overloading of the standard definition since it also includes points that move out-of-frame. Estimating the motion of these points is extremely difficult, particularly in the two-frame setting. Previous work relies on CNNs to learn occlusions, without much success, or requires multiple frames to reason about occlusions using temporal smoothness. In this paper, we argue that the occlusion problem can be better solved in the two-frame case by modelling image self-similarities. We introduce a global motion aggregation module, a transformer-based approach to find long-range dependencies between pixels in the first image, and perform global aggregation on the corresponding motion features. We demonstrate that the optical flow estimates in the occluded regions can be significantly improved without damaging the performance in non-occluded regions. This approach obtains new state-of-the-art results on the challenging Sintel dataset, improving the average end-point error by 13.6\% on Sintel Final and 13.7\% on Sintel Clean. At the time of submission, our method ranks first on these benchmarks among all published and unpublished approaches. Code is available at https://github.com/zacjiang/GMA .

Learning Optical Flow from a Few Matches

State-of-the-art neural network models for optical flow estimation require a dense correlation volume at high resolutions for representing per-pixel displacement. Although the dense correlation volume is informative for accurate estimation, its heavy computation and memory usage hinders the efficient training and deployment of the models. In this paper, we show that the dense correlation volume representation is redundant and accurate flow estimation can be achieved with only a fraction of elements in it. Based on this observation, we propose an alternative displacement representation, named Sparse Correlation Volume, which is constructed directly by computing the k closest matches in one feature map for each feature vector in the other feature map and stored in a sparse data structure. Experiments show that our method can reduce computational cost and memory use significantly, while maintaining high accuracy compared to previous approaches with dense correlation volumes. Code is available at https://github.com/zacjiang/scv .

Joint Unsupervised Learning of Optical Flow and Egomotion with Bi-Level Optimization

We address the problem of joint optical flow and camera motion estimation in rigid scenes by incorporating geometric constraints into an unsupervised deep learning framework. Unlike existing approaches which rely on brightness constancy and local smoothness for optical flow estimation, we exploit the global relationship between optical flow and camera motion using epipolar geometry. In particular, we formulate the prediction of optical flow and camera motion as a bi-level optimization problem, consisting of an upper-level problem to estimate the flow that conforms to the predicted camera motion, and a lower-level problem to estimate the camera motion given the predicted optical flow. We use implicit differentiation to enable back-propagation through the lower-level geometric optimization layer independent of its implementation, allowing end-to-end training of the network. With globally-enforced geometric constraints, we are able to improve the quality of the estimated optical flow in challenging scenarios and obtain better camera motion estimates compared to other unsupervised learning methods.