Rhythm Transcription of Polyphonic Piano Music Based on Merged-Output HMM for Multiple Voices

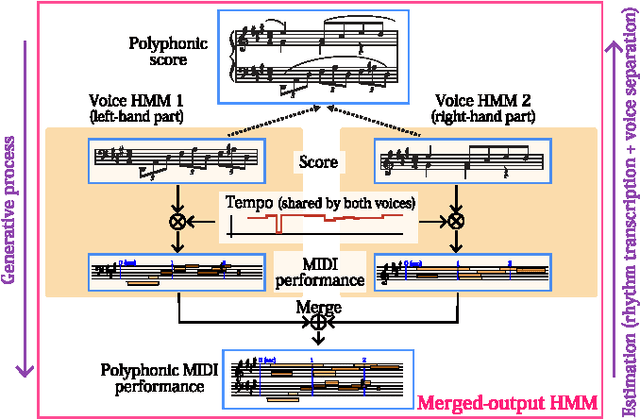
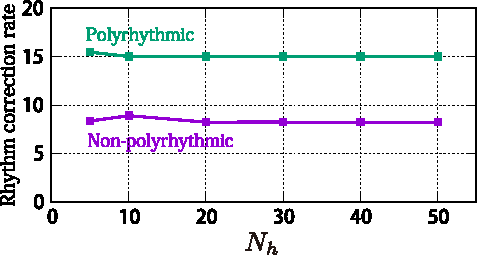
In a recent conference paper, we have reported a rhythm transcription method based on a merged-output hidden Markov model (HMM) that explicitly describes the multiple-voice structure of polyphonic music. This model solves a major problem of conventional methods that could not properly describe the nature of multiple voices as in polyrhythmic scores or in the phenomenon of loose synchrony between voices. In this paper we present a complete description of the proposed model and develop an inference technique, which is valid for any merged-output HMMs for which output probabilities depend on past events. We also examine the influence of the architecture and parameters of the method in terms of accuracies of rhythm transcription and voice separation and perform comparative evaluations with six other algorithms. Using MIDI recordings of classical piano pieces, we found that the proposed model outperformed other methods by more than 12 points in the accuracy for polyrhythmic performances and performed almost as good as the best one for non-polyrhythmic performances. This reveals the state-of-the-art methods of rhythm transcription for the first time in the literature. Publicly available source codes are also provided for future comparisons.

A Stochastic Temporal Model of Polyphonic MIDI Performance with Ornaments

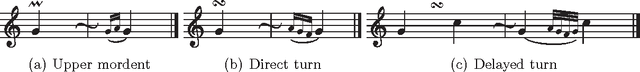
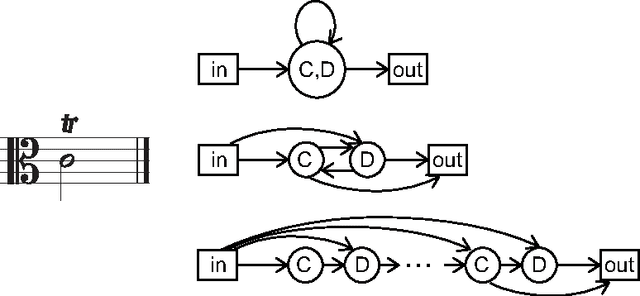
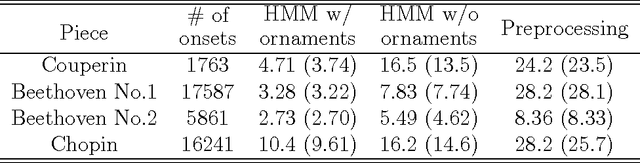
We study indeterminacies in realization of ornaments and how they can be incorporated in a stochastic performance model applicable for music information processing such as score-performance matching. We point out the importance of temporal information, and propose a hidden Markov model which describes it explicitly and represents ornaments with several state types. Following a review of the indeterminacies, they are carefully incorporated into the model through its topology and parameters, and the state construction for quite general polyphonic scores is explained in detail. By analyzing piano performance data, we find significant overlaps in inter-onset-interval distributions of chordal notes, ornaments, and inter-chord events, and the data is used to determine details of the model. The model is applied for score following and offline score-performance matching, yielding highly accurate matching for performances with many ornaments and relatively frequent errors, repeats, and skips.

Real-Time Audio-to-Score Alignment of Music Performances Containing Errors and Arbitrary Repeats and Skips

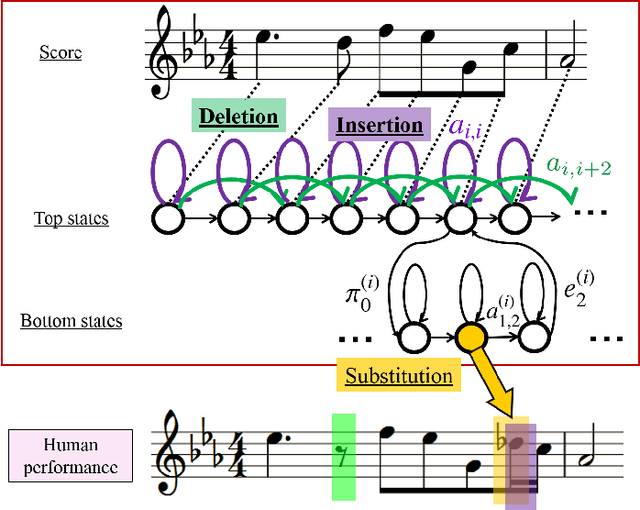
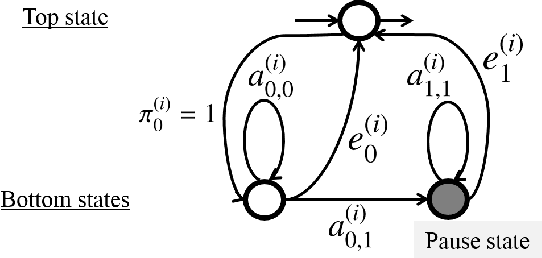
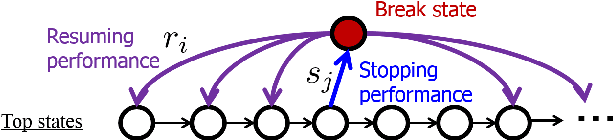
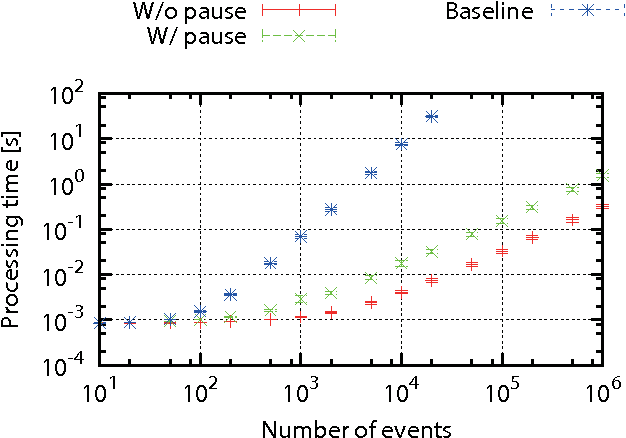
This paper discusses real-time alignment of audio signals of music performance to the corresponding score (a.k.a. score following) which can handle tempo changes, errors and arbitrary repeats and/or skips (repeats/skips) in performances. This type of score following is particularly useful in automatic accompaniment for practices and rehearsals, where errors and repeats/skips are often made. Simple extensions of the algorithms previously proposed in the literature are not applicable in these situations for scores of practical length due to the problem of large computational complexity. To cope with this problem, we present two hidden Markov models of monophonic performance with errors and arbitrary repeats/skips, and derive efficient score-following algorithms with an assumption that the prior probability distributions of score positions before and after repeats/skips are independent from each other. We confirmed real-time operation of the algorithms with music scores of practical length (around 10000 notes) on a modern laptop and their tracking ability to the input performance within 0.7 s on average after repeats/skips in clarinet performance data. Further improvements and extension for polyphonic signals are also discussed.

Outer-Product Hidden Markov Model and Polyphonic MIDI Score Following

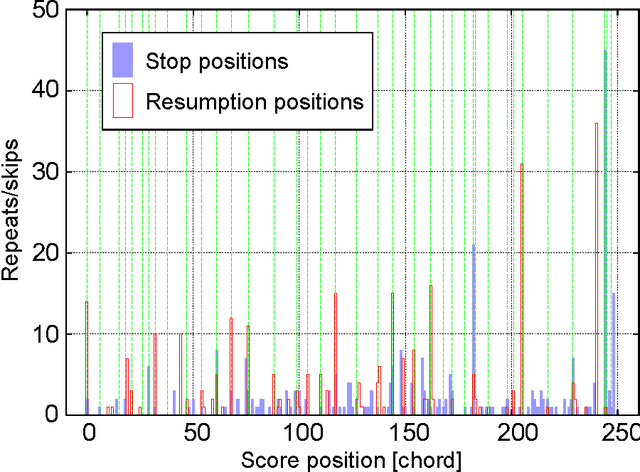
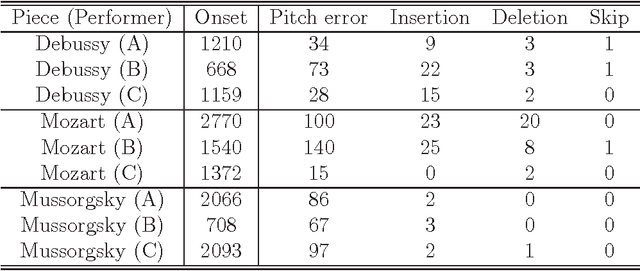
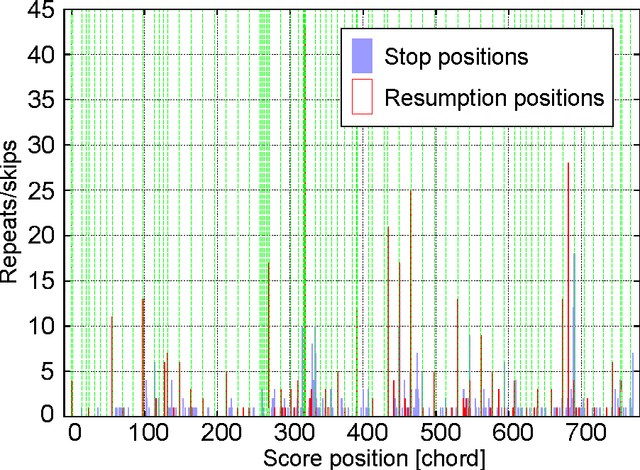
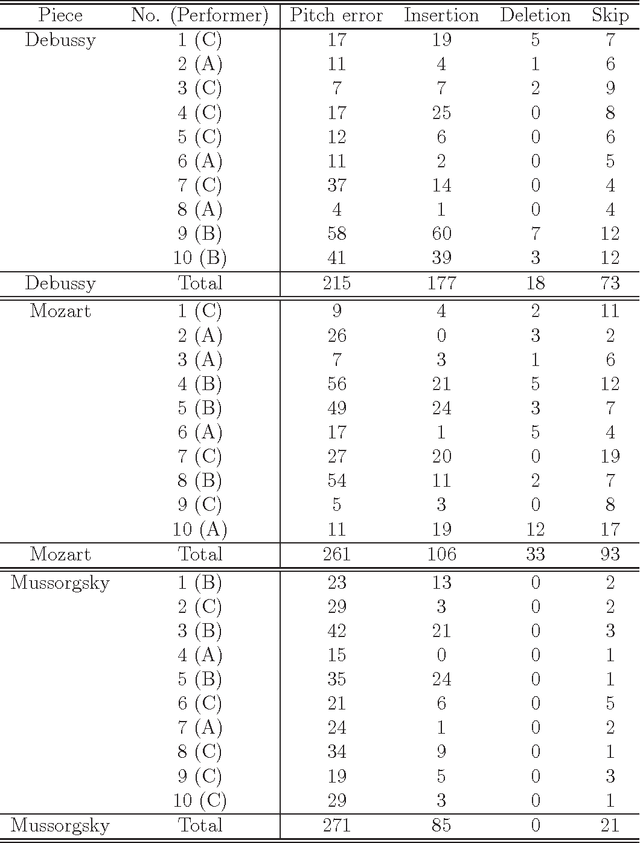
We present a polyphonic MIDI score-following algorithm capable of following performances with arbitrary repeats and skips, based on a probabilistic model of musical performances. It is attractive in practical applications of score following to handle repeats and skips which may be made arbitrarily during performances, but the algorithms previously described in the literature cannot be applied to scores of practical length due to problems with large computational complexity. We propose a new type of hidden Markov model (HMM) as a performance model which can describe arbitrary repeats and skips including performer tendencies on distributed score positions before and after them, and derive an efficient score-following algorithm that reduces computational complexity without pruning. A theoretical discussion on how much such information on performer tendencies improves the score-following results is given. The proposed score-following algorithm also admits performance mistakes and is demonstrated to be effective in practical situations by carrying out evaluations with human performances. The proposed HMM is potentially valuable for other topics in information processing and we also provide a detailed description of inference algorithms.