Outer-Product Hidden Markov Model and Polyphonic MIDI Score Following

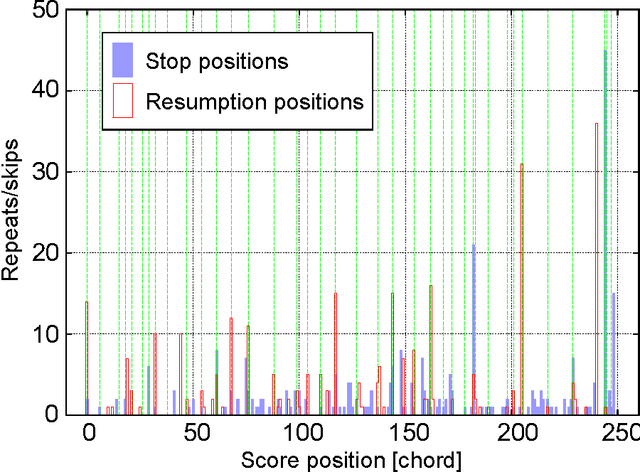
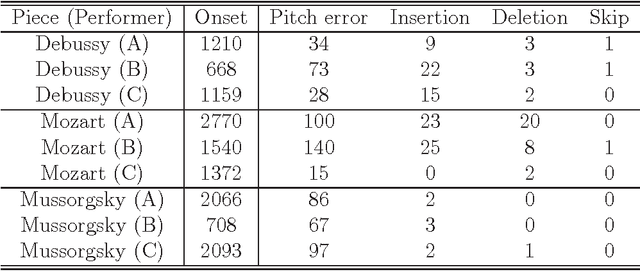
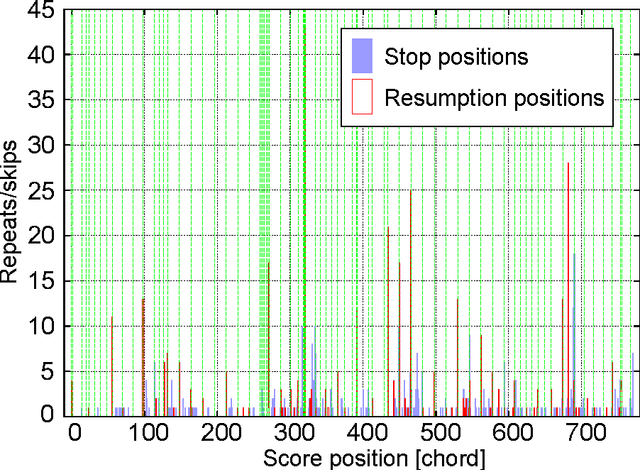
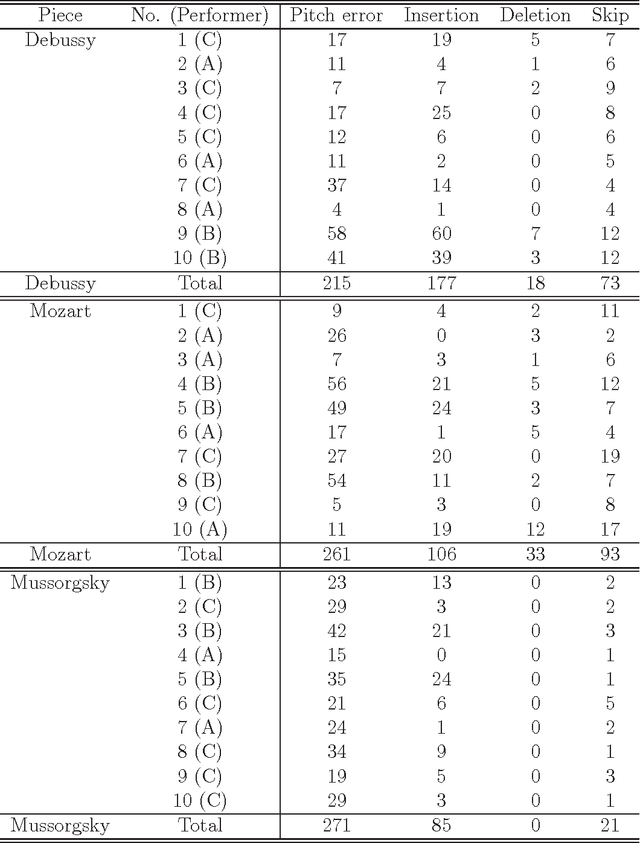
We present a polyphonic MIDI score-following algorithm capable of following performances with arbitrary repeats and skips, based on a probabilistic model of musical performances. It is attractive in practical applications of score following to handle repeats and skips which may be made arbitrarily during performances, but the algorithms previously described in the literature cannot be applied to scores of practical length due to problems with large computational complexity. We propose a new type of hidden Markov model (HMM) as a performance model which can describe arbitrary repeats and skips including performer tendencies on distributed score positions before and after them, and derive an efficient score-following algorithm that reduces computational complexity without pruning. A theoretical discussion on how much such information on performer tendencies improves the score-following results is given. The proposed score-following algorithm also admits performance mistakes and is demonstrated to be effective in practical situations by carrying out evaluations with human performances. The proposed HMM is potentially valuable for other topics in information processing and we also provide a detailed description of inference algorithms.