Yasuyuki Saito
Statistical Learning and Estimation of Piano Fingering
Apr 23, 2019
Abstract:Automatic estimation of piano fingering is important for computationally understanding the process of music performance and applicable to performance assistance and education systems. While a natural way to formulate the quality of fingerings is to construct models of the constraints/costs of performance, it is generally difficult to find appropriate parameter values for these models. Here we study an alternative data-driven approach based on statistical modeling in which the naturalness of a given fingering is described by probabilities. Specifically, we construct two types of hidden Markov models (HMMs) and their higher-order extensions. We also study deep neural network (DNN)-based methods for comparison. Using a newly released dataset of fingering annotations, we conduct systematic evaluations of these models as well as a representative constraint-based method and find that the methods based on high-order HMMs outperform others in terms of estimation accuracies. We also quantitatively study individual difference of fingering and propose evaluation measures that can be used with multiple ground truth data. We conclude that the HMM-based methods are currently state of the art and generate acceptable fingerings in most parts and that they have certain limitations such as ignorance of phrase boundaries and interdependence of the two hands.
Outer-Product Hidden Markov Model and Polyphonic MIDI Score Following
Apr 08, 2014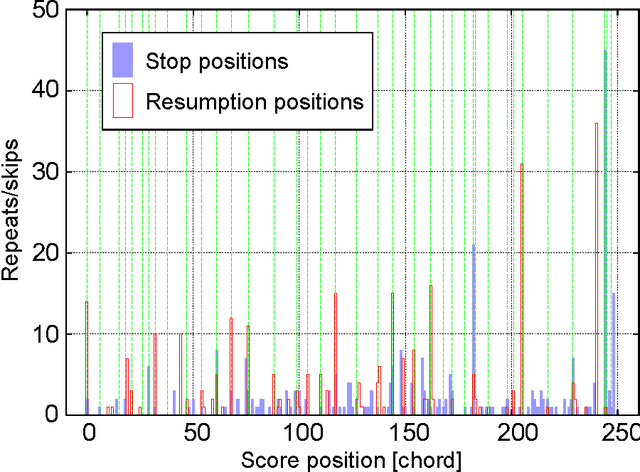
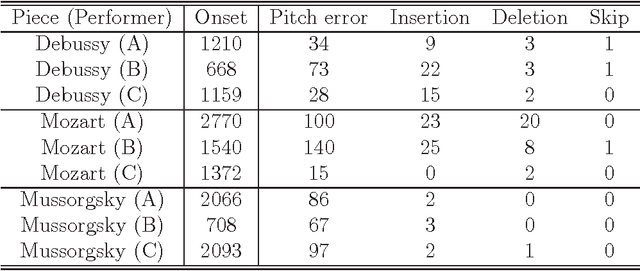
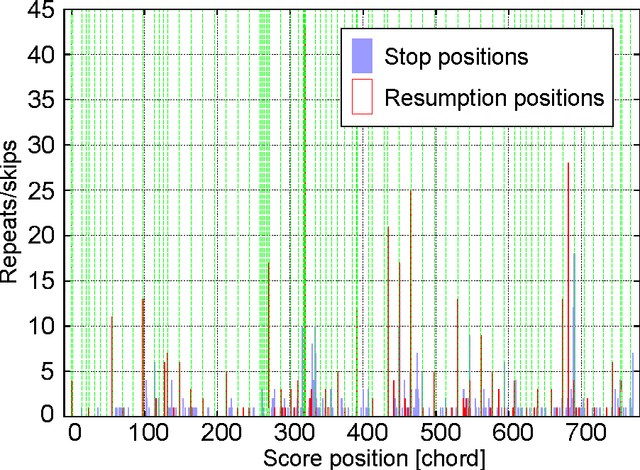
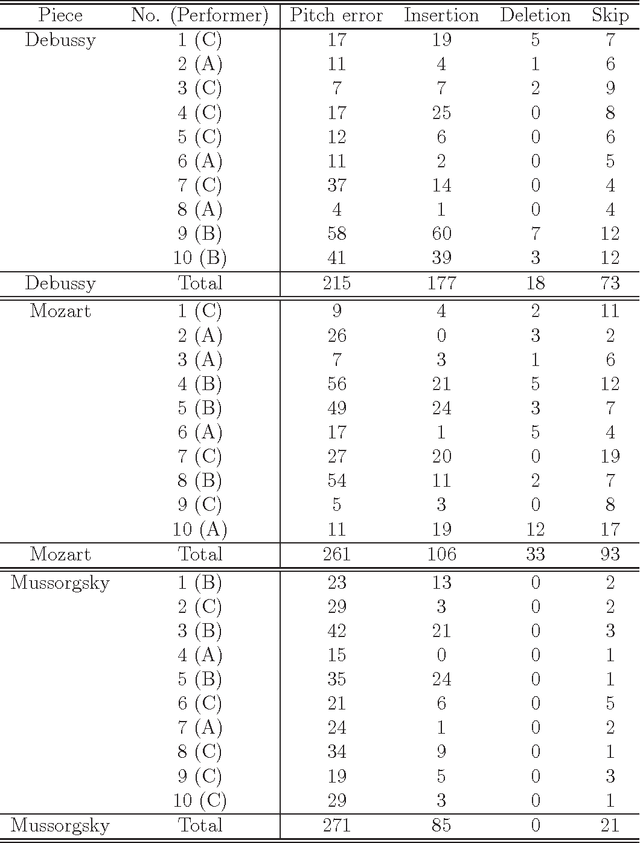
Abstract:We present a polyphonic MIDI score-following algorithm capable of following performances with arbitrary repeats and skips, based on a probabilistic model of musical performances. It is attractive in practical applications of score following to handle repeats and skips which may be made arbitrarily during performances, but the algorithms previously described in the literature cannot be applied to scores of practical length due to problems with large computational complexity. We propose a new type of hidden Markov model (HMM) as a performance model which can describe arbitrary repeats and skips including performer tendencies on distributed score positions before and after them, and derive an efficient score-following algorithm that reduces computational complexity without pruning. A theoretical discussion on how much such information on performer tendencies improves the score-following results is given. The proposed score-following algorithm also admits performance mistakes and is demonstrated to be effective in practical situations by carrying out evaluations with human performances. The proposed HMM is potentially valuable for other topics in information processing and we also provide a detailed description of inference algorithms.
* 42 pages, 8 figures, version submitted to JNMR. To appear in Journal of New Music Research (2014)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge