Coupled Splines for Sparse Curve Fitting

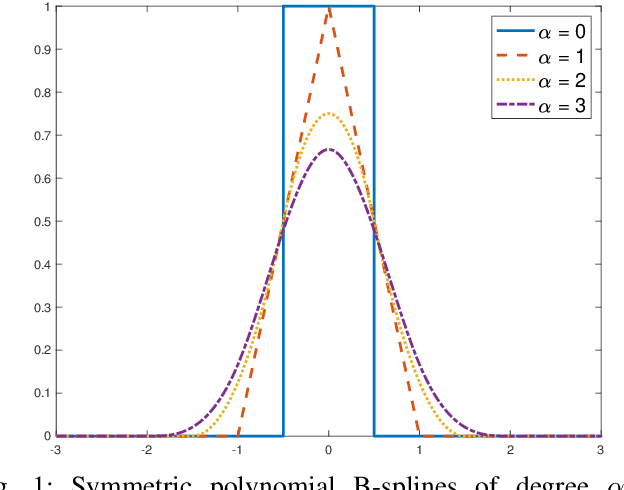
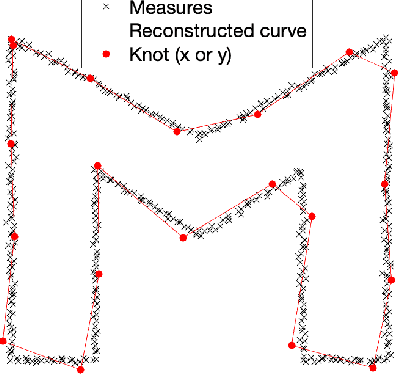
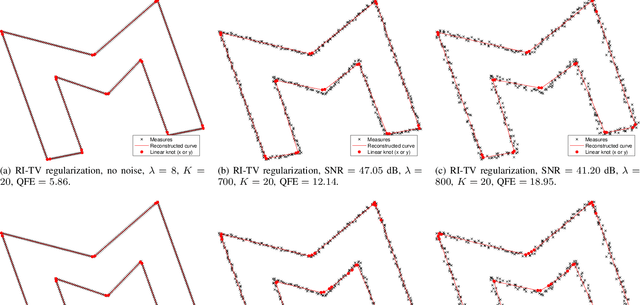
We formulate as an inverse problem the construction of sparse parametric continuous curve models that fit a sequence of contour points. Our prior is incorporated as a regularization term that encourages rotation invariance and sparsity. We prove that an optimal solution to the inverse problem is a closed curve with spline components. We then show how to efficiently solve the task using B-splines as basis functions. We extend our problem formulation to curves made of two distinct components with complementary smoothness properties and solve it using hybrid splines. We illustrate the performance of our model on contours of different smoothness. Our experimental results show that we can faithfully reconstruct any general contour using few parameters, even in the presence of imprecisions in the measurements.

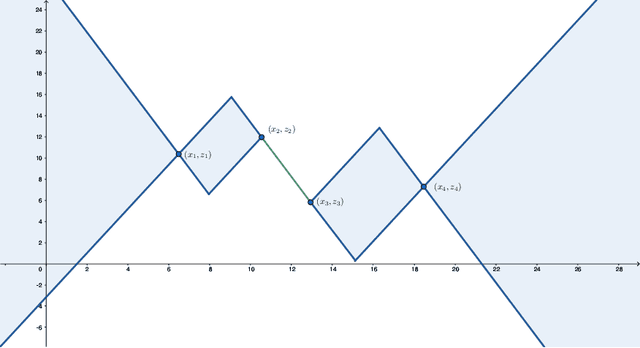
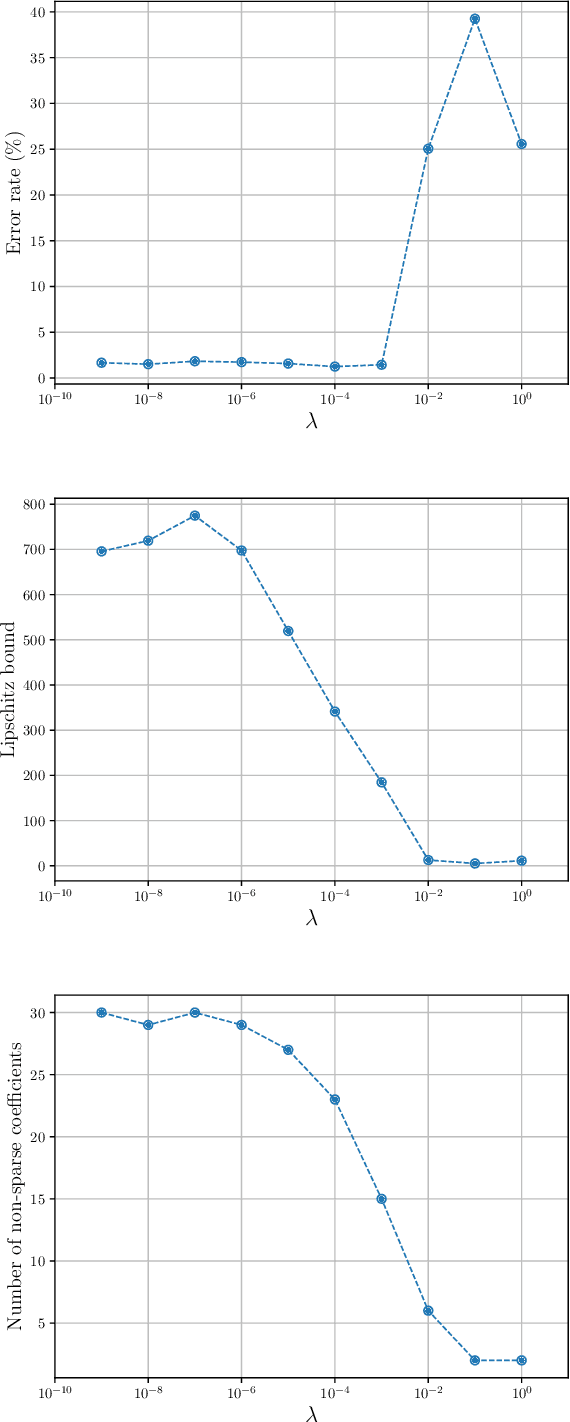
Sparsest Univariate Learning Models Under Lipschitz Constraint

Beside the minimization of the prediction error, two of the most desirable properties of a regression scheme are stability and interpretability. Driven by these principles, we propose continuous-domain formulations for one-dimensional regression problems. In our first approach, we use the Lipschitz constant as a regularizer, which results in an implicit tuning of the overall robustness of the learned mapping. In our second approach, we control the Lipschitz constant explicitly using a user-defined upper-bound and make use of a sparsity-promoting regularizer to favor simpler (and, hence, more interpretable) solutions. The theoretical study of the latter formulation is motivated in part by its equivalence, which we prove, with the training of a Lipschitz-constrained two-layer univariate neural network with rectified linear unit (ReLU) activations and weight decay. By proving representer theorems, we show that both problems admit global minimizers that are continuous and piecewise-linear (CPWL) functions. Moreover, we propose efficient algorithms that find the sparsest solution of each problem: the CPWL mapping with the least number of linear regions. Finally, we illustrate numerically the outcome of our formulations.

Measuring Complexity of Learning Schemes Using Hessian-Schatten Total-Variation

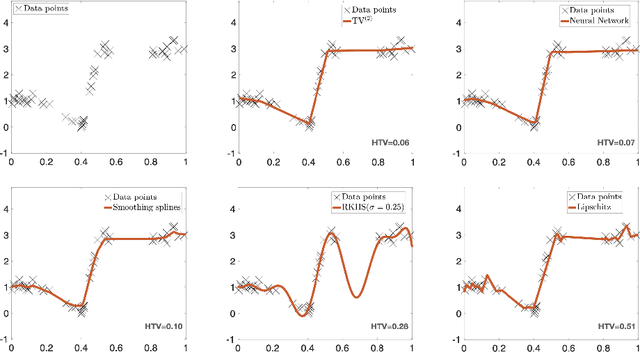
In this paper, we introduce the Hessian-Schatten total-variation (HTV) -- a novel seminorm that quantifies the total "rugosity" of multivariate functions. Our motivation for defining HTV is to assess the complexity of supervised learning schemes. We start by specifying the adequate matrix-valued Banach spaces that are equipped with suitable classes of mixed-norms. We then show that HTV is invariant to rotations, scalings, and translations. Additionally, its minimum value is achieved for linear mappings, supporting the common intuition that linear regression is the least complex learning model. Next, we present closed-form expressions for computing the HTV of two general classes of functions. The first one is the class of Sobolev functions with a certain degree of regularity, for which we show that HTV coincides with the Hessian-Schatten seminorm that is sometimes used as a regularizer for image reconstruction. The second one is the class of continuous and piecewise linear (CPWL) functions. In this case, we show that the HTV reflects the total change in slopes between linear regions that have a common facet. Hence, it can be viewed as a convex relaxation (l1-type) of the number of linear regions (l0-type) of CPWL mappings. Finally, we illustrate the use of our proposed seminorm with some concrete examples.

Continuous-Domain Formulation of Inverse Problems for Composite Sparse-Plus-Smooth Signals

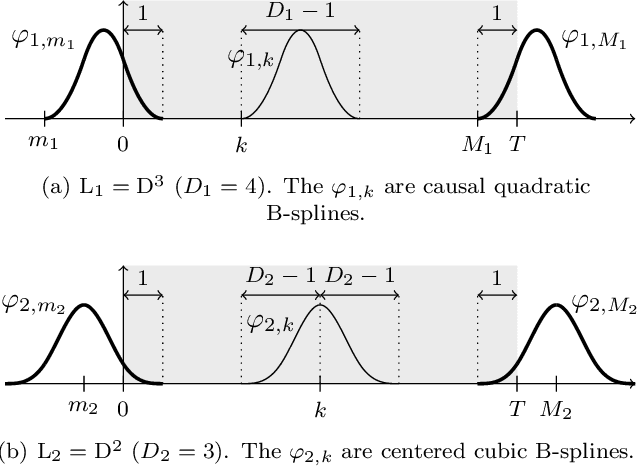
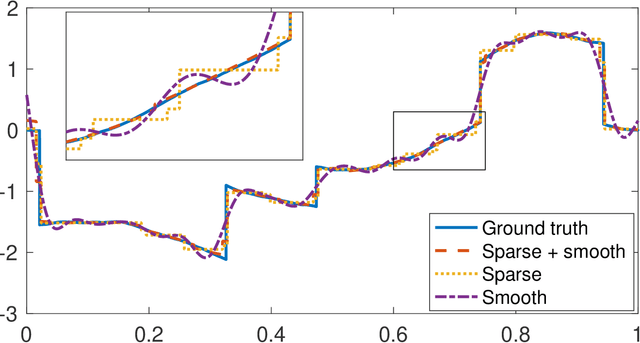
We present a novel framework for the reconstruction of 1D composite signals assumed to be a mixture of two additive components, one sparse and the other smooth, given a finite number of linear measurements. We formulate the reconstruction problem as a continuous-domain regularized inverse problem with multiple penalties. We prove that these penalties induce reconstructed signals that indeed take the desired form of the sum of a sparse and a smooth component. We then discretize this problem using Riesz bases, which yields a discrete problem that can be solved by standard algorithms. Our discretization is exact in the sense that we are solving the continuous-domain problem over the search space specified by our bases without any discretization error. We propose a complete algorithmic pipeline and demonstrate its feasibility on simulated data.

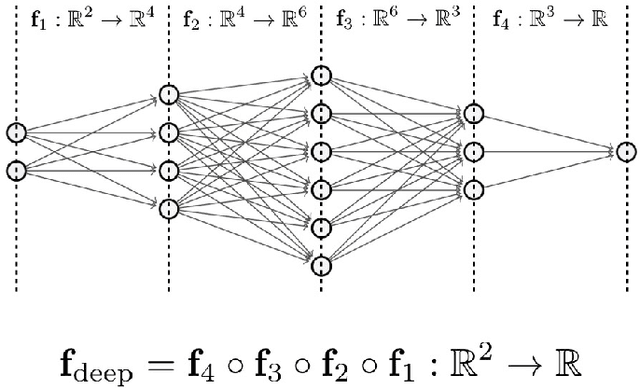
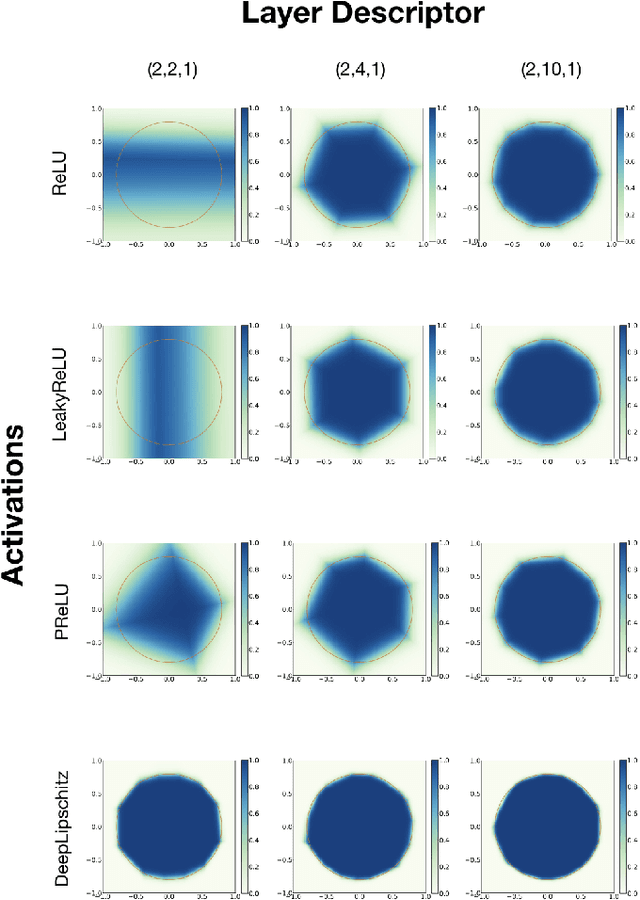
Deep Neural Networks with Trainable Activations and Controlled Lipschitz Constant

We introduce a variational framework to learn the activation functions of deep neural networks. The main motivation is to control the Lipschitz regularity of the input-output relation. To that end, we first establish a global bound for the Lipschitz constant of neural networks. Based on the obtained bound, we then formulate a variational problem for learning activation functions. Our variational problem is infinite-dimensional and is not computationally tractable. However, we prove that there always exists a solution that has continuous and piecewise-linear (linear-spline) activations. This reduces the original problem to a finite-dimensional minimization. We numerically compare our scheme with standard ReLU network and its variations, PReLU and LeakyReLU.

An L1 Representer Theorem for Multiple-Kernel Regression

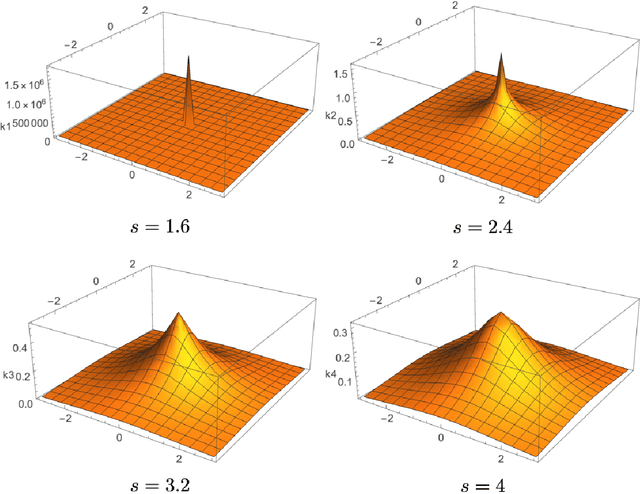
The theory of RKHS provides an elegant framework for supervised learning. It is the foundation of all kernel methods in machine learning. Implicit in its formulation is the use of a quadratic regularizer associated with the underlying inner product which imposes smoothness constraints. In this paper, we consider instead the generalized total-variation (gTV) norm as the sparsity-promoting regularizer. This leads us to propose a new Banach-space framework that justifies the use of generalized LASSO, albeit in a slightly modified version. We prove a representer theorem for multiple-kernel regression (MKR) with gTV regularization. The theorem states that the solutions of MKR have kernel expansions with adaptive positions, while the gTV norm enforces an $\ell_1$ penalty on the coefficients. We discuss the sparsity-promoting effect of the gTV norm which prevents redundancy in the multiple-kernel scenario.