Deep Neural Networks with Trainable Activations and Controlled Lipschitz Constant
Paper and Code
Jan 17, 2020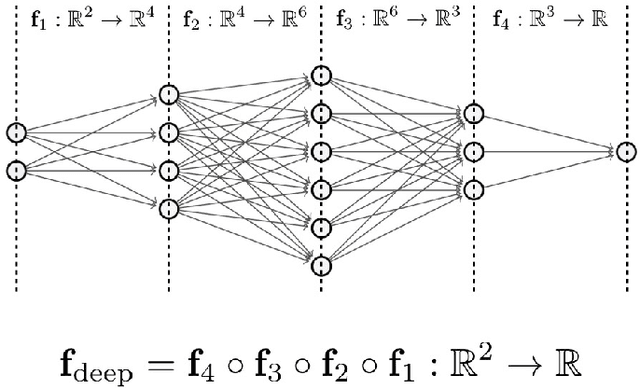
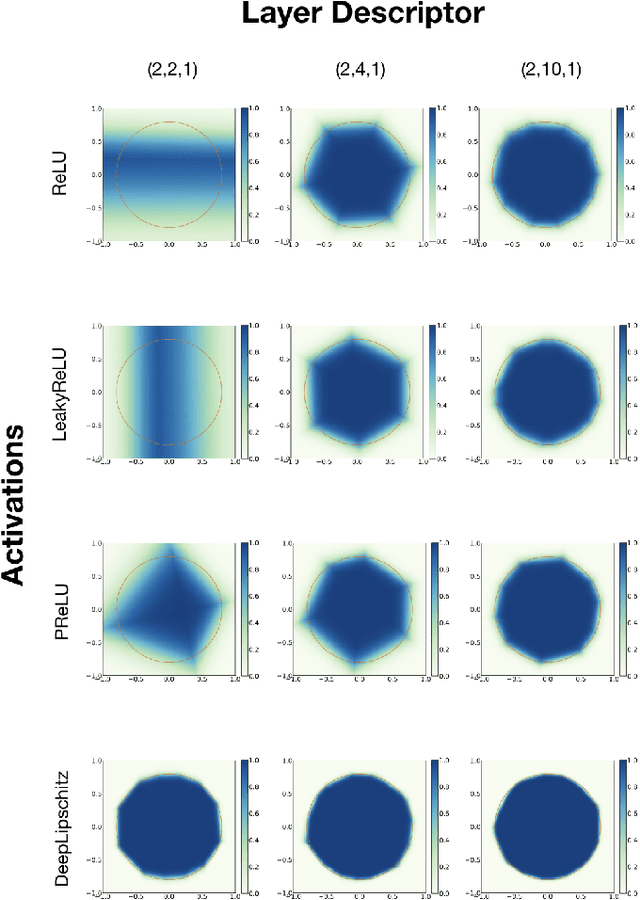
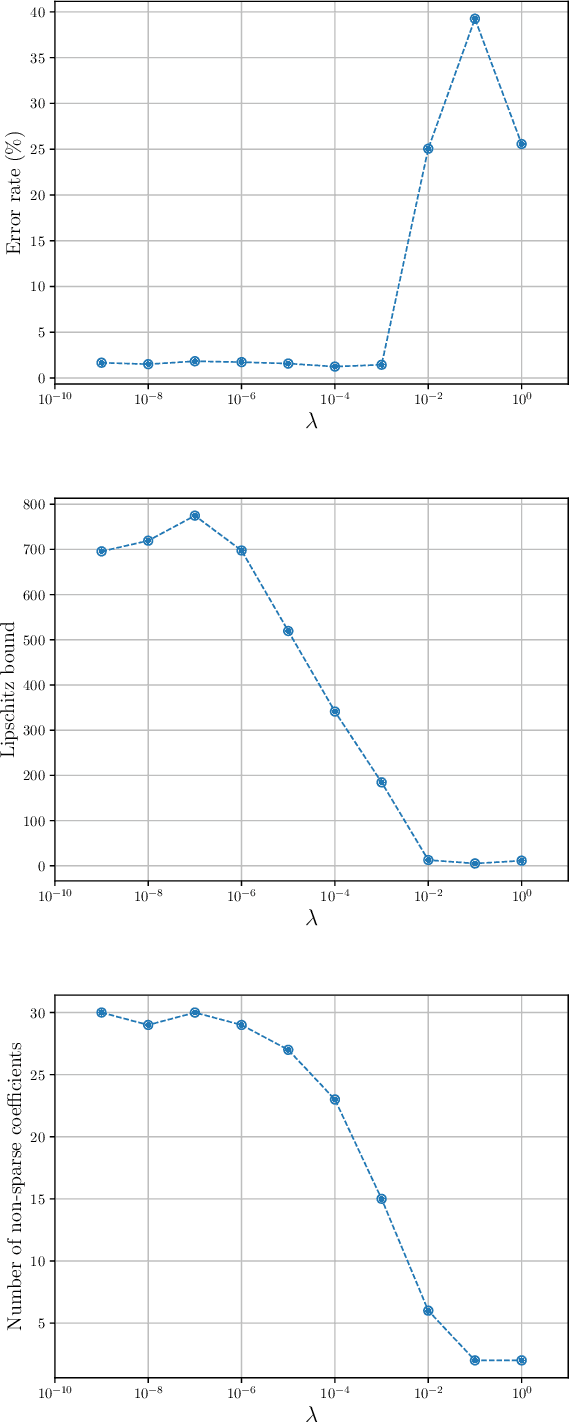
We introduce a variational framework to learn the activation functions of deep neural networks. The main motivation is to control the Lipschitz regularity of the input-output relation. To that end, we first establish a global bound for the Lipschitz constant of neural networks. Based on the obtained bound, we then formulate a variational problem for learning activation functions. Our variational problem is infinite-dimensional and is not computationally tractable. However, we prove that there always exists a solution that has continuous and piecewise-linear (linear-spline) activations. This reduces the original problem to a finite-dimensional minimization. We numerically compare our scheme with standard ReLU network and its variations, PReLU and LeakyReLU.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge