Measuring Complexity of Learning Schemes Using Hessian-Schatten Total-Variation

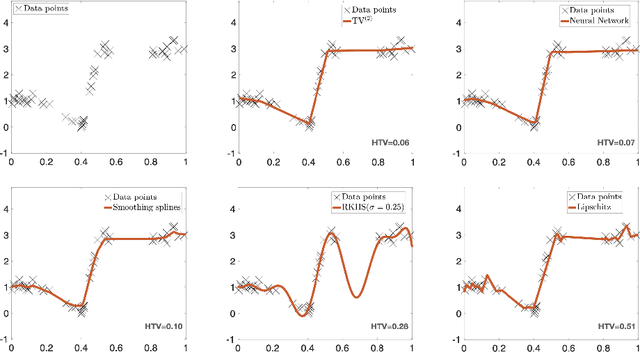
In this paper, we introduce the Hessian-Schatten total-variation (HTV) -- a novel seminorm that quantifies the total "rugosity" of multivariate functions. Our motivation for defining HTV is to assess the complexity of supervised learning schemes. We start by specifying the adequate matrix-valued Banach spaces that are equipped with suitable classes of mixed-norms. We then show that HTV is invariant to rotations, scalings, and translations. Additionally, its minimum value is achieved for linear mappings, supporting the common intuition that linear regression is the least complex learning model. Next, we present closed-form expressions for computing the HTV of two general classes of functions. The first one is the class of Sobolev functions with a certain degree of regularity, for which we show that HTV coincides with the Hessian-Schatten seminorm that is sometimes used as a regularizer for image reconstruction. The second one is the class of continuous and piecewise linear (CPWL) functions. In this case, we show that the HTV reflects the total change in slopes between linear regions that have a common facet. Hence, it can be viewed as a convex relaxation (l1-type) of the number of linear regions (l0-type) of CPWL mappings. Finally, we illustrate the use of our proposed seminorm with some concrete examples.

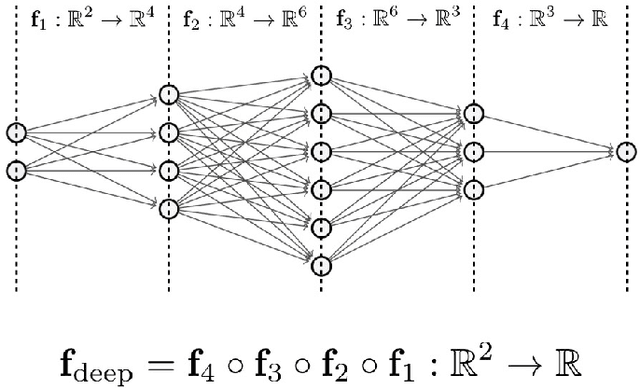
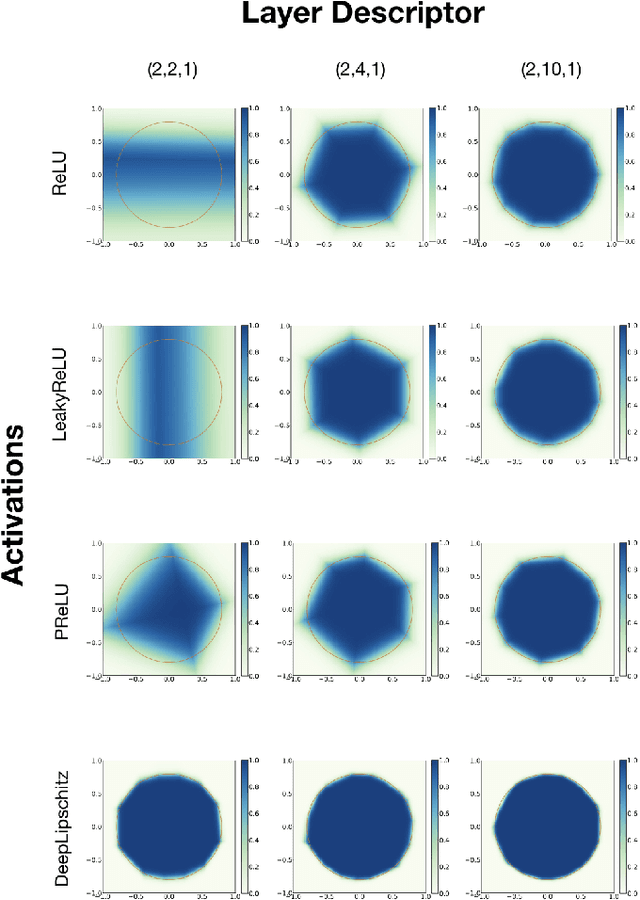
Deep Neural Networks with Trainable Activations and Controlled Lipschitz Constant

We introduce a variational framework to learn the activation functions of deep neural networks. The main motivation is to control the Lipschitz regularity of the input-output relation. To that end, we first establish a global bound for the Lipschitz constant of neural networks. Based on the obtained bound, we then formulate a variational problem for learning activation functions. Our variational problem is infinite-dimensional and is not computationally tractable. However, we prove that there always exists a solution that has continuous and piecewise-linear (linear-spline) activations. This reduces the original problem to a finite-dimensional minimization. We numerically compare our scheme with standard ReLU network and its variations, PReLU and LeakyReLU.

Content Adaptive Optimization for Neural Image Compression

The field of neural image compression has witnessed exciting progress as recently proposed architectures already surpass the established transform coding based approaches. While, so far, research has mainly focused on architecture and model improvements, in this work we explore content adaptive optimization. To this end, we introduce an iterative procedure which adapts the latent representation to the specific content we wish to compress while keeping the parameters of the network and the predictive model fixed. Our experiments show that this allows for an overall increase in rate-distortion performance, independently of the specific architecture used. Furthermore, we also evaluate this strategy in the context of adapting a pretrained network to other content that is different in visual appearance or resolution. Here, our experiments show that our adaptation strategy can largely close the gap as compared to models specifically trained for the given content while having the benefit that no additional data in the form of model parameter updates has to be transmitted.