Measuring Complexity of Learning Schemes Using Hessian-Schatten Total-Variation
Paper and Code
Dec 12, 2021

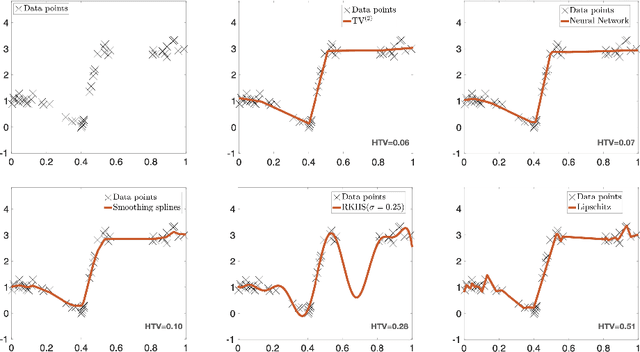

In this paper, we introduce the Hessian-Schatten total-variation (HTV) -- a novel seminorm that quantifies the total "rugosity" of multivariate functions. Our motivation for defining HTV is to assess the complexity of supervised learning schemes. We start by specifying the adequate matrix-valued Banach spaces that are equipped with suitable classes of mixed-norms. We then show that HTV is invariant to rotations, scalings, and translations. Additionally, its minimum value is achieved for linear mappings, supporting the common intuition that linear regression is the least complex learning model. Next, we present closed-form expressions for computing the HTV of two general classes of functions. The first one is the class of Sobolev functions with a certain degree of regularity, for which we show that HTV coincides with the Hessian-Schatten seminorm that is sometimes used as a regularizer for image reconstruction. The second one is the class of continuous and piecewise linear (CPWL) functions. In this case, we show that the HTV reflects the total change in slopes between linear regions that have a common facet. Hence, it can be viewed as a convex relaxation (l1-type) of the number of linear regions (l0-type) of CPWL mappings. Finally, we illustrate the use of our proposed seminorm with some concrete examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge