Sparsest Univariate Learning Models Under Lipschitz Constraint
Paper and Code
Dec 27, 2021


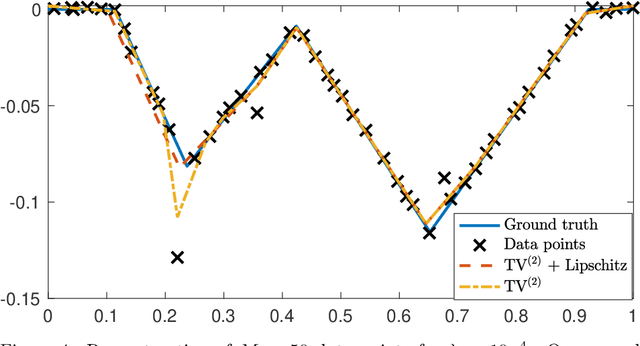
Beside the minimization of the prediction error, two of the most desirable properties of a regression scheme are stability and interpretability. Driven by these principles, we propose continuous-domain formulations for one-dimensional regression problems. In our first approach, we use the Lipschitz constant as a regularizer, which results in an implicit tuning of the overall robustness of the learned mapping. In our second approach, we control the Lipschitz constant explicitly using a user-defined upper-bound and make use of a sparsity-promoting regularizer to favor simpler (and, hence, more interpretable) solutions. The theoretical study of the latter formulation is motivated in part by its equivalence, which we prove, with the training of a Lipschitz-constrained two-layer univariate neural network with rectified linear unit (ReLU) activations and weight decay. By proving representer theorems, we show that both problems admit global minimizers that are continuous and piecewise-linear (CPWL) functions. Moreover, we propose efficient algorithms that find the sparsest solution of each problem: the CPWL mapping with the least number of linear regions. Finally, we illustrate numerically the outcome of our formulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge