Shaofei Qin
Dominant Patterns: Critical Features Hidden in Deep Neural Networks
May 31, 2021


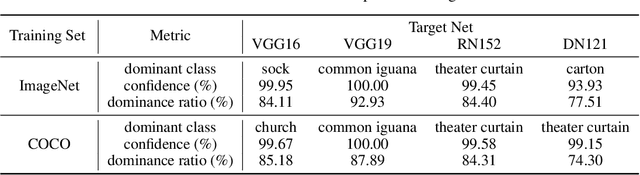
Abstract:In this paper, we find the existence of critical features hidden in Deep NeuralNetworks (DNNs), which are imperceptible but can actually dominate the outputof DNNs. We call these features dominant patterns. As the name suggests, for a natural image, if we add the dominant pattern of a DNN to it, the output of this DNN is determined by the dominant pattern instead of the original image, i.e., DNN's prediction is the same with the dominant pattern's. We design an algorithm to find such patterns by pursuing the insensitivity in the feature space. A direct application of the dominant patterns is the Universal Adversarial Perturbations(UAPs). Numerical experiments show that the found dominant patterns defeat state-of-the-art UAP methods, especially in label-free settings. In addition, dominant patterns are proved to have the potential to attack downstream tasks in which DNNs share the same backbone. We claim that DNN-specific dominant patterns reveal some essential properties of a DNN and are of great importance for its feature analysis and robustness enhancement.
Quaternion Product Units for Deep Learning on 3D Rotation Groups
Dec 17, 2019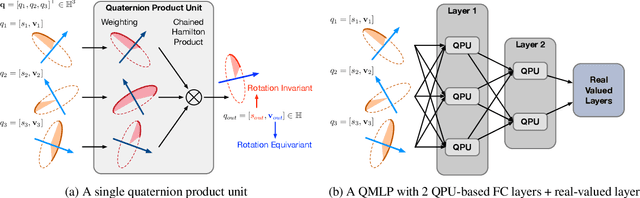

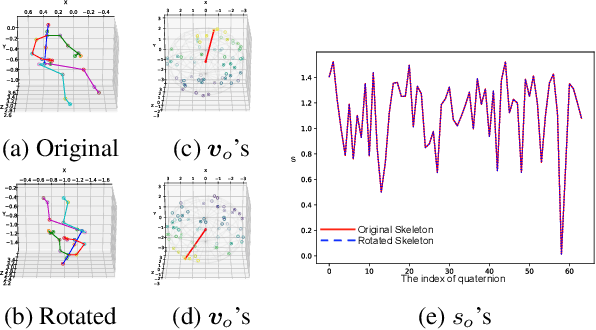

Abstract:We propose a novel quaternion product unit (QPU) to represent data on 3D rotation groups. The QPU leverages quaternion algebra and the law of 3D rotation group, representing 3D rotation data as quaternions and merging them via a weighted chain of Hamilton products. We prove that the representations derived by the proposed QPU can be disentangled into "rotation-invariant" features and "rotation-equivariant" features, respectively, which supports the rationality and the efficiency of the QPU in theory. We design quaternion neural networks based on our QPUs and make our models compatible with existing deep learning models. Experiments on both synthetic and real-world data show that the proposed QPU is beneficial for the learning tasks requiring rotation robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge