Quaternion Product Units for Deep Learning on 3D Rotation Groups
Paper and Code
Dec 17, 2019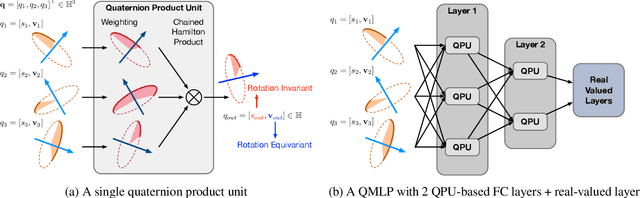


We propose a novel quaternion product unit (QPU) to represent data on 3D rotation groups. The QPU leverages quaternion algebra and the law of 3D rotation group, representing 3D rotation data as quaternions and merging them via a weighted chain of Hamilton products. We prove that the representations derived by the proposed QPU can be disentangled into "rotation-invariant" features and "rotation-equivariant" features, respectively, which supports the rationality and the efficiency of the QPU in theory. We design quaternion neural networks based on our QPUs and make our models compatible with existing deep learning models. Experiments on both synthetic and real-world data show that the proposed QPU is beneficial for the learning tasks requiring rotation robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge