Cooperative Multi-Satellite ISAC Networks: Centralized vs. Distributed Sensing

This paper investigates a downlink multi-satellite integrated sensing and communication (ISAC) network, in which multiple satellites simultaneously transmit ISAC signals to provide communication services to ground user equipments and enable cooperative sensing of airborne targets through multiple gateways. To support this dual functionality, we introduce communication and sensing beamforming designs based on uniform planar arrays with optimized power allocation. Building on these designs, we propose two cooperative sensing frameworks, namely centralized and distributed. In the centralized framework, each gateway forwards its sensing observations to a central unit (CU), where the positions of multiple targets are jointly estimated from the aggregated data using a sparse signal recovery formulation. To mitigate the signaling overhead inherent in centralized processing, a distributed framework is further proposed, in which each gateway independently estimates target positions and transmits only the local estimates to the CU. To associate estimates from different gateways, a data association problem based on the squared Euclidean distance is formulated and efficiently solved using the Hungarian algorithm. The final target positions are then obtained by minimizing the distance estimation error. Simulation results demonstrate that the proposed centralized and distributed frameworks significantly outperform existing sensing schemes while satisfying communication performance requirements. We also evaluate the sensing-communication trade-off from the viewpoints of sensing accuracy and communication power consumption under the proposed frameworks.

MIMO Detection under Hardware Impairments: Learning with Noisy Labels

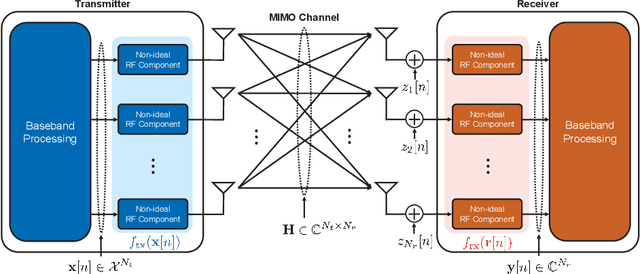
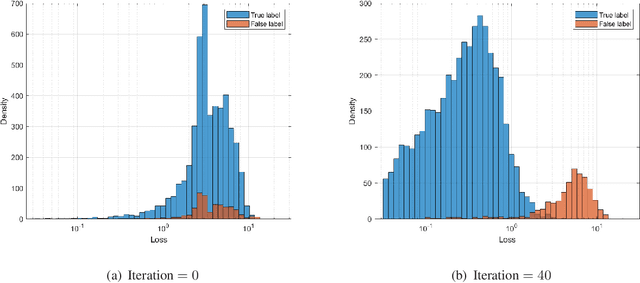
This paper considers a data detection problem in multiple-input multiple-output (MIMO) communication systems with hardware impairments. To address challenges posed by nonlinear and unknown distortion in received signals, two learning-based detection methods, referred to as model-driven and data-driven, are presented. The model-driven method employs a generalized Gaussian distortion model to approximate the conditional distribution of the distorted received signal. By using the outputs of coarse data detection as noisy training data, the model-driven method avoids the need for additional training overhead beyond traditional pilot overhead for channel estimation. An expectation-maximization algorithm is devised to accurately learn the parameters of the distortion model from noisy training data. To resolve a model mismatch problem in the model-driven method, the data-driven method employs a deep neural network (DNN) for approximating a-posteriori probabilities for each received signal. This method uses the outputs of the model-driven method as noisy labels and therefore does not require extra training overhead. To avoid the overfitting problem caused by noisy labels, a robust DNN training algorithm is devised, which involves a warm-up period, sample selection, and loss correction. Simulation results demonstrate that the two proposed methods outperform existing solutions with the same overhead under various hardware impairment scenarios.

Noise-adding Methods of Saliency Map as Series of Higher Order Partial Derivative

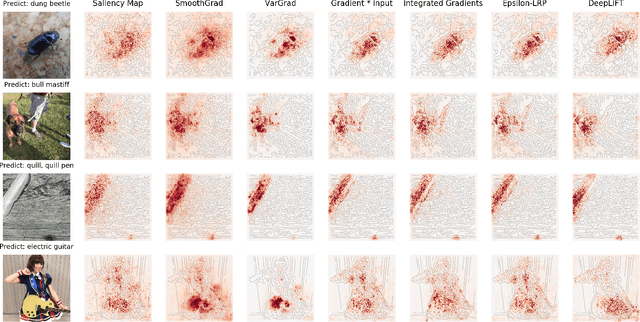
SmoothGrad and VarGrad are techniques that enhance the empirical quality of standard saliency maps by adding noise to input. However, there were few works that provide a rigorous theoretical interpretation of those methods. We analytically formalize the result of these noise-adding methods. As a result, we observe two interesting results from the existing noise-adding methods. First, SmoothGrad does not make the gradient of the score function smooth. Second, VarGrad is independent of the gradient of the score function. We believe that our findings provide a clue to reveal the relationship between local explanation methods of deep neural networks and higher-order partial derivatives of the score function.