Quantum median filter for Total Variation image denoising

In this new computing paradigm, named quantum computing, researchers from all over the world are taking their first steps in designing quantum circuits for image processing, through a difficult process of knowledge transfer. This effort is named Quantum Image Processing, an emerging research field pushed by powerful parallel computing capabilities of quantum computers. This work goes in this direction and proposes the challenging development of a powerful method of image denoising, such as the Total Variation (TV) model, in a quantum environment. The proposed Quantum TV is described and its sub-components are analysed. Despite the natural limitations of the current capabilities of quantum devices, the experimental results show a competitive denoising performance compared to the classical variational TV counterpart.

Non-convex Super-resolution of OCT images via sparse representation

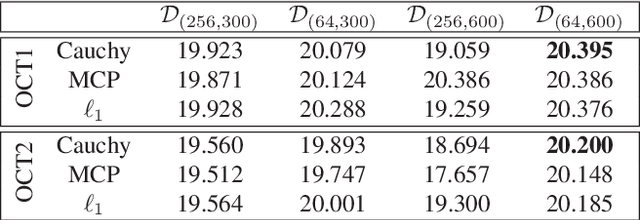
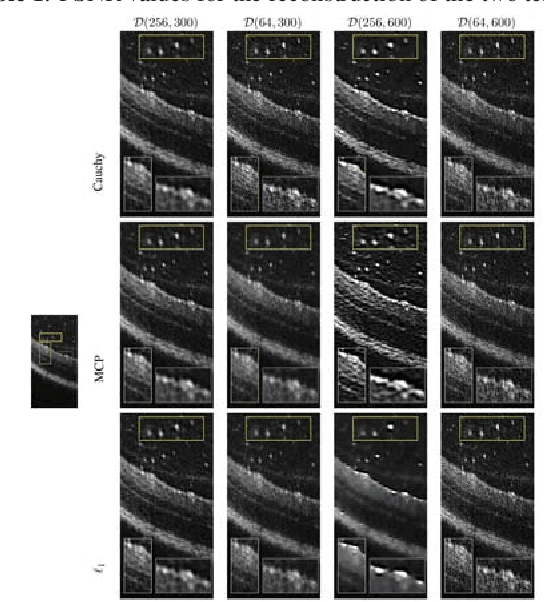
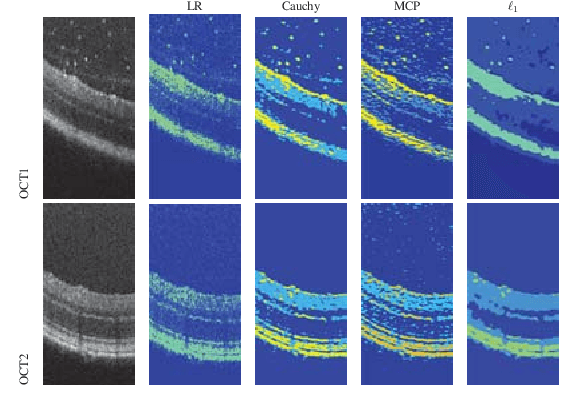
We propose a non-convex variational model for the super-resolution of Optical Coherence Tomography (OCT) images of the murine eye, by enforcing sparsity with respect to suitable dictionaries learnt from high-resolution OCT data. The statistical characteristics of OCT images motivate the use of {\alpha}-stable distributions for learning dictionaries, by considering the non-Gaussian case, {\alpha}=1. The sparsity-promoting cost function relies on a non-convex penalty - Cauchy-based or Minimax Concave Penalty (MCP) - which makes the problem particularly challenging. We propose an efficient algorithm for minimizing the function based on the forward-backward splitting strategy which guarantees at each iteration the existence and uniqueness of the proximal point. Comparisons with standard convex L1-based reconstructions show the better performance of non-convex models, especially in view of further OCT image analysis

Vessel Segmentation in Medical Imaging Using a Tight-Frame Based Algorithm

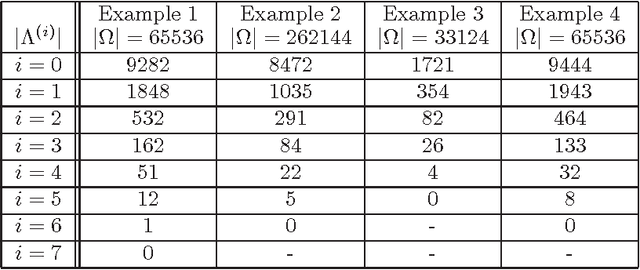
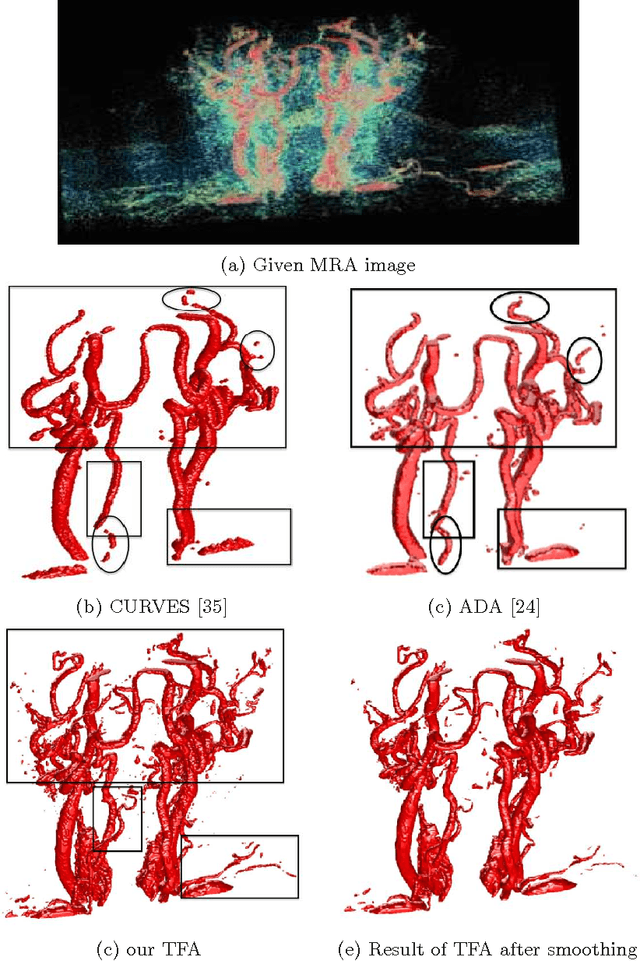
Tight-frame, a generalization of orthogonal wavelets, has been used successfully in various problems in image processing, including inpainting, impulse noise removal, super-resolution image restoration, etc. Segmentation is the process of identifying object outlines within images. There are quite a few efficient algorithms for segmentation that depend on the variational approach and the partial differential equation (PDE) modeling. In this paper, we propose to apply the tight-frame approach to automatically identify tube-like structures such as blood vessels in Magnetic Resonance Angiography (MRA) images. Our method iteratively refines a region that encloses the possible boundary or surface of the vessels. In each iteration, we apply the tight-frame algorithm to denoise and smooth the possible boundary and sharpen the region. We prove the convergence of our algorithm. Numerical experiments on real 2D/3D MRA images demonstrate that our method is very efficient with convergence usually within a few iterations, and it outperforms existing PDE and variational methods as it can extract more tubular objects and fine details in the images.