Space-adaptive anisotropic bivariate Laplacian regularization for image restoration

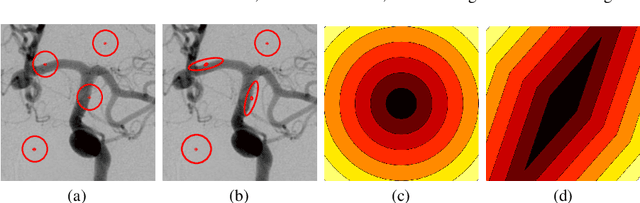
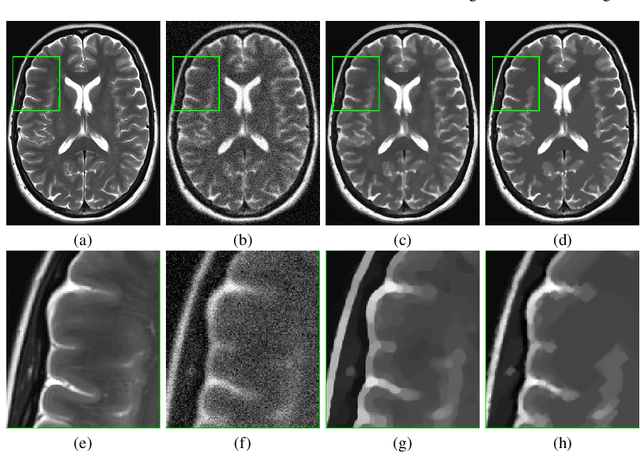
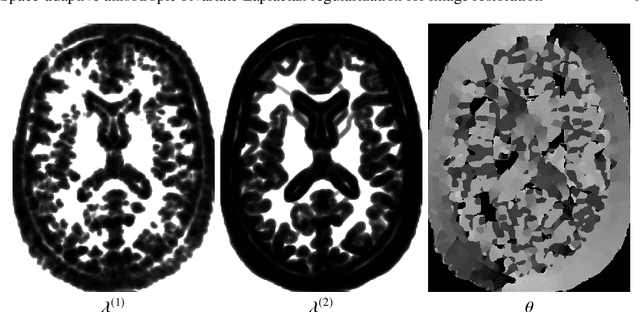
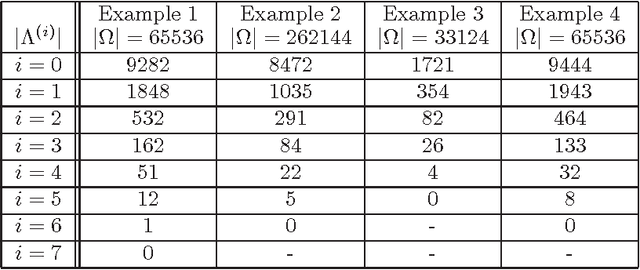
In this paper we present a new regularization term for variational image restoration which can be regarded as a space-variant anisotropic extension of the classical isotropic Total Variation (TV) regularizer. The proposed regularizer comes from the statistical assumption that the gradients of the target image distribute locally according to space-variant bivariate Laplacian distributions. The highly flexible variational structure of the corresponding regularizer encodes several free parameters which hold the potential for faithfully modelling the local geometry in the image and describing local orientation preferences. For an automatic estimation of such parameters, we design a robust maximum likelihood approach and report results on its reliability on synthetic data and natural images. A minimization algorithm based on the Alternating Direction Method of Multipliers (ADMM) is presented for the efficient numerical solution of the proposed variational model. Some experimental results are reported which demonstrate the high-quality of restorations achievable by the proposed model, in particular with respect to classical Total Variation regularization.

Vessel Segmentation in Medical Imaging Using a Tight-Frame Based Algorithm

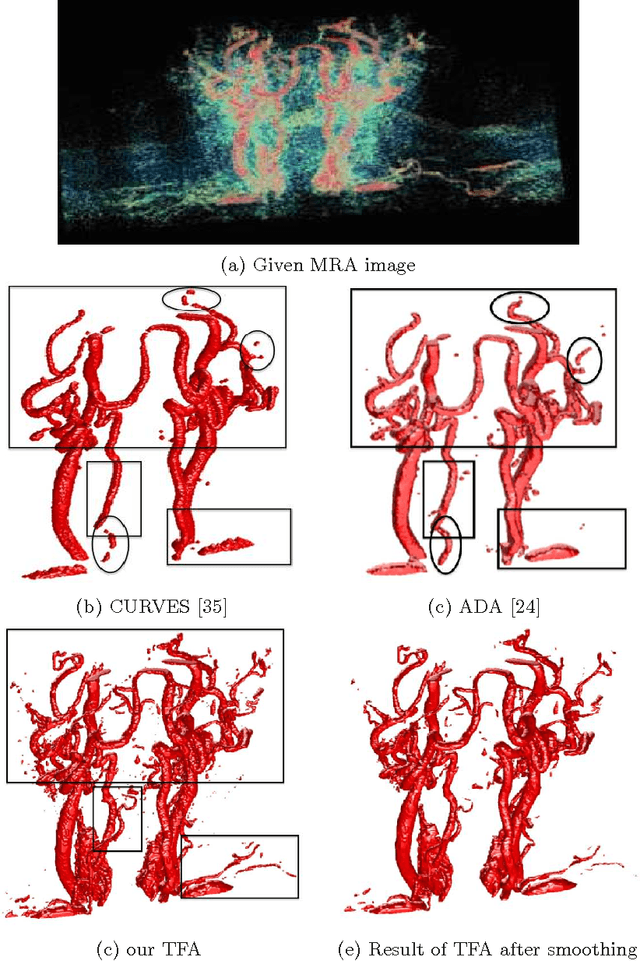
Tight-frame, a generalization of orthogonal wavelets, has been used successfully in various problems in image processing, including inpainting, impulse noise removal, super-resolution image restoration, etc. Segmentation is the process of identifying object outlines within images. There are quite a few efficient algorithms for segmentation that depend on the variational approach and the partial differential equation (PDE) modeling. In this paper, we propose to apply the tight-frame approach to automatically identify tube-like structures such as blood vessels in Magnetic Resonance Angiography (MRA) images. Our method iteratively refines a region that encloses the possible boundary or surface of the vessels. In each iteration, we apply the tight-frame algorithm to denoise and smooth the possible boundary and sharpen the region. We prove the convergence of our algorithm. Numerical experiments on real 2D/3D MRA images demonstrate that our method is very efficient with convergence usually within a few iterations, and it outperforms existing PDE and variational methods as it can extract more tubular objects and fine details in the images.