Monica Pragliola
Whiteness-based bilevel estimation of weighted TV parameter maps for image denoising
Mar 10, 2025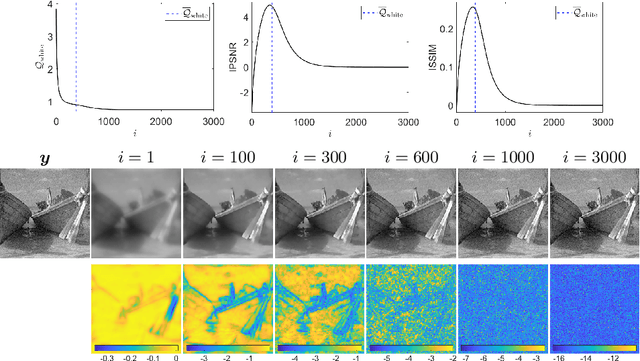
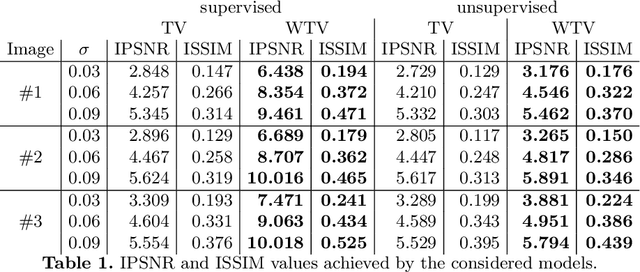

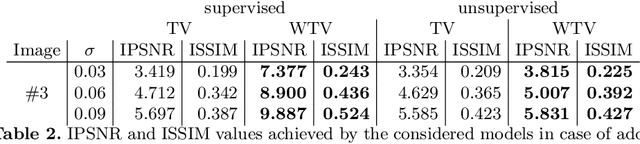
Abstract:We consider a bilevel optimisation strategy based on normalised residual whiteness loss for estimating the weighted total variation parameter maps for denoising images corrupted by additive white Gaussian noise. Compared to supervised and semi-supervised approaches relying on prior knowledge of (approximate) reference data and/or information on the noise magnitude, the proposal is fully unsupervised. To avoid noise overfitting an early stopping strategy is used, relying on simple statistics of optimal performances on a set of natural images. Numerical results comparing the supervised/unsupervised procedures for scalar/pixel-dependent \mbox{parameter maps are shown.
Whiteness-based bilevel learning of regularization parameters in imaging
Mar 10, 2024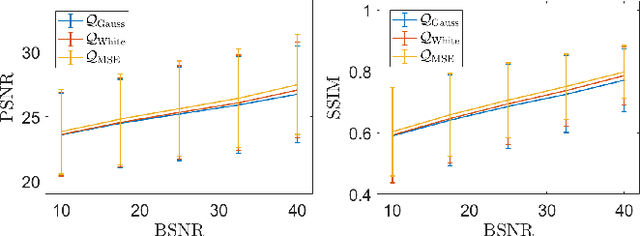
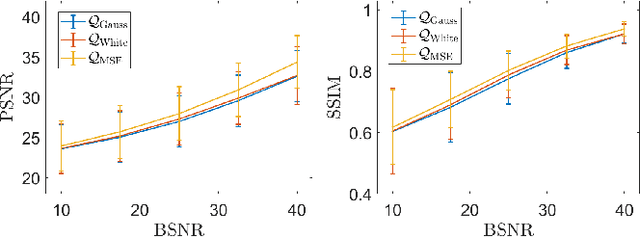
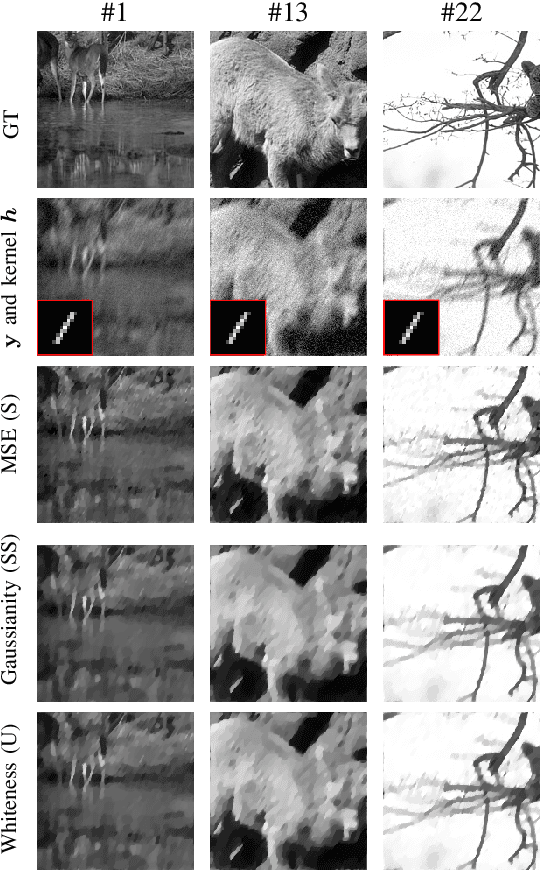

Abstract:We consider an unsupervised bilevel optimization strategy for learning regularization parameters in the context of imaging inverse problems in the presence of additive white Gaussian noise. Compared to supervised and semi-supervised metrics relying either on the prior knowledge of reference data and/or on some (partial) knowledge on the noise statistics, the proposed approach optimizes the whiteness of the residual between the observed data and the observation model with no need of ground-truth data.We validate the approach on standard Total Variation-regularized image deconvolution problems which show that the proposed quality metric provides estimates close to the mean-square error oracle and to discrepancy-based principles.
Space-adaptive anisotropic bivariate Laplacian regularization for image restoration
Aug 02, 2019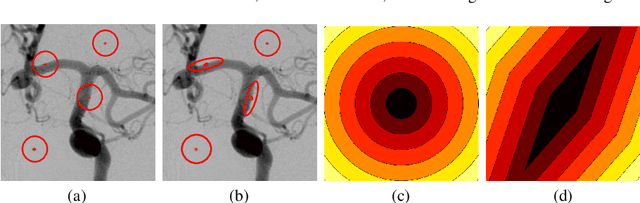

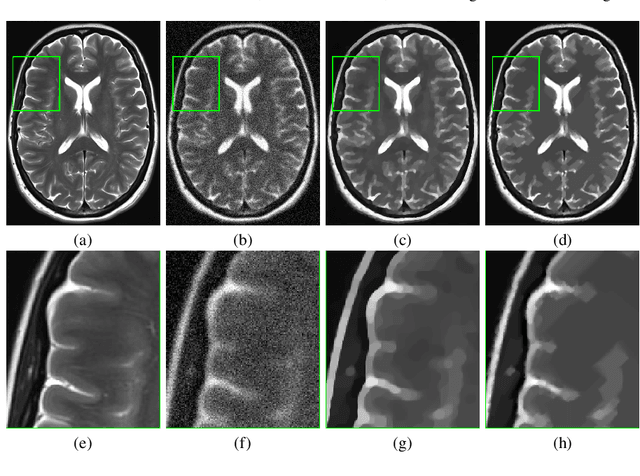
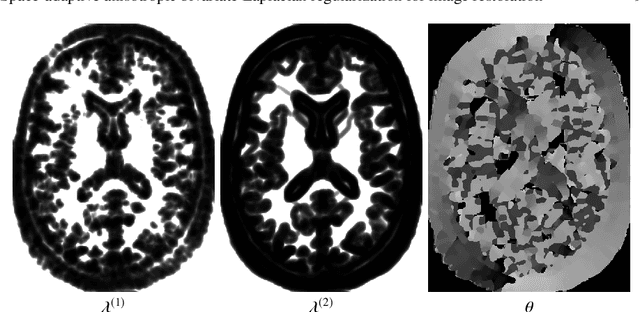
Abstract:In this paper we present a new regularization term for variational image restoration which can be regarded as a space-variant anisotropic extension of the classical isotropic Total Variation (TV) regularizer. The proposed regularizer comes from the statistical assumption that the gradients of the target image distribute locally according to space-variant bivariate Laplacian distributions. The highly flexible variational structure of the corresponding regularizer encodes several free parameters which hold the potential for faithfully modelling the local geometry in the image and describing local orientation preferences. For an automatic estimation of such parameters, we design a robust maximum likelihood approach and report results on its reliability on synthetic data and natural images. A minimization algorithm based on the Alternating Direction Method of Multipliers (ADMM) is presented for the efficient numerical solution of the proposed variational model. Some experimental results are reported which demonstrate the high-quality of restorations achievable by the proposed model, in particular with respect to classical Total Variation regularization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge