A Variational Approach for Joint Image Recovery and Features Extraction Based on Spatially Varying Generalised Gaussian Models

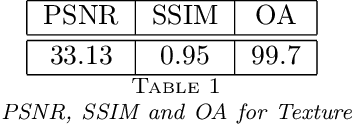
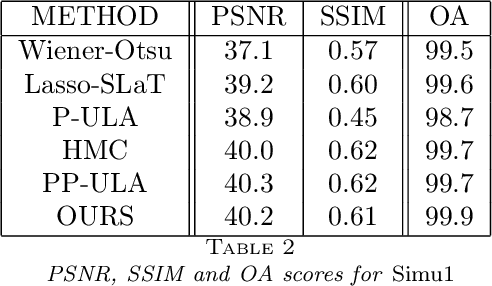
The joint problem of reconstruction / feature extraction is a challenging task in image processing. It consists in performing, in a joint manner, the restoration of an image and the extraction of its features. In this work, we firstly propose a novel nonsmooth and nonconvex variational formulation of the problem. For this purpose, we introduce a versatile generalised Gaussian prior whose parameters, including its exponent, are space-variant. Secondly, we design an alternating proximal-based optimisation algorithm that efficiently exploits the structure of the proposed nonconvex objective function. We also analyze the convergence of this algorithm. As shown in numerical experiments conducted on joint segmentation/deblurring tasks, the proposed method provides high-quality results.

Non-convex Super-resolution of OCT images via sparse representation

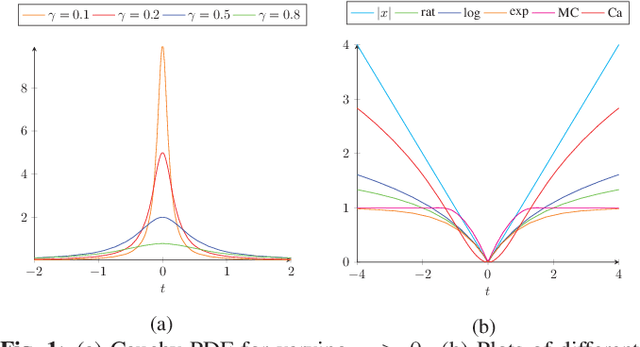
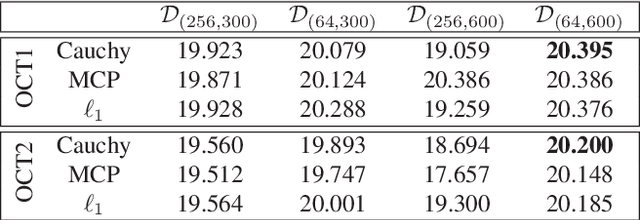
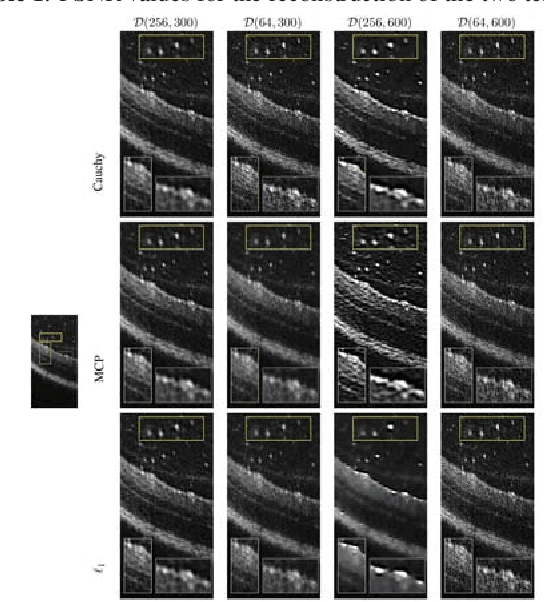
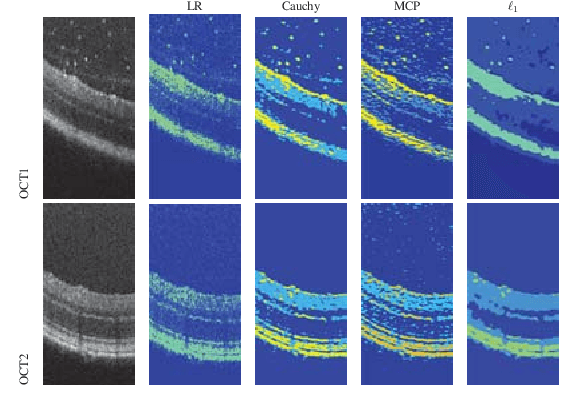
We propose a non-convex variational model for the super-resolution of Optical Coherence Tomography (OCT) images of the murine eye, by enforcing sparsity with respect to suitable dictionaries learnt from high-resolution OCT data. The statistical characteristics of OCT images motivate the use of {\alpha}-stable distributions for learning dictionaries, by considering the non-Gaussian case, {\alpha}=1. The sparsity-promoting cost function relies on a non-convex penalty - Cauchy-based or Minimax Concave Penalty (MCP) - which makes the problem particularly challenging. We propose an efficient algorithm for minimizing the function based on the forward-backward splitting strategy which guarantees at each iteration the existence and uniqueness of the proximal point. Comparisons with standard convex L1-based reconstructions show the better performance of non-convex models, especially in view of further OCT image analysis