Mechanistically Interpreting a Transformer-based 2-SAT Solver: An Axiomatic Approach

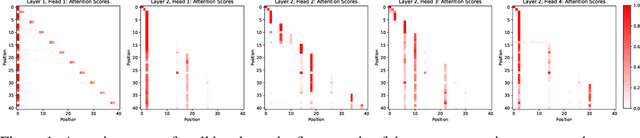
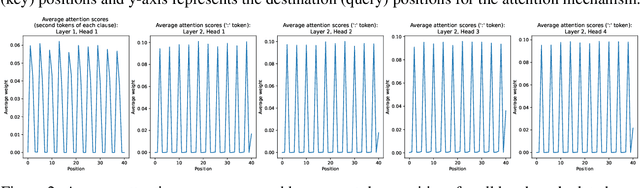
Mechanistic interpretability aims to reverse engineer the computation performed by a neural network in terms of its internal components. Although there is a growing body of research on mechanistic interpretation of neural networks, the notion of a mechanistic interpretation itself is often ad-hoc. Inspired by the notion of abstract interpretation from the program analysis literature that aims to develop approximate semantics for programs, we give a set of axioms that formally characterize a mechanistic interpretation as a description that approximately captures the semantics of the neural network under analysis in a compositional manner. We use these axioms to guide the mechanistic interpretability analysis of a Transformer-based model trained to solve the well-known 2-SAT problem. We are able to reverse engineer the algorithm learned by the model -- the model first parses the input formulas and then evaluates their satisfiability via enumeration of different possible valuations of the Boolean input variables. We also present evidence to support that the mechanistic interpretation of the analyzed model indeed satisfies the stated axioms.

Learning Modulo Theories

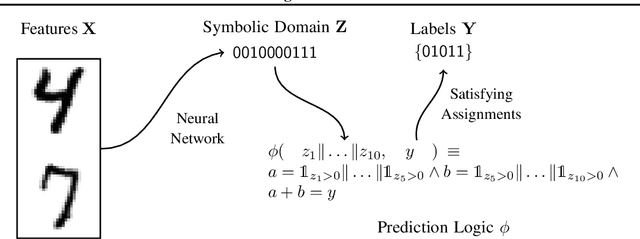
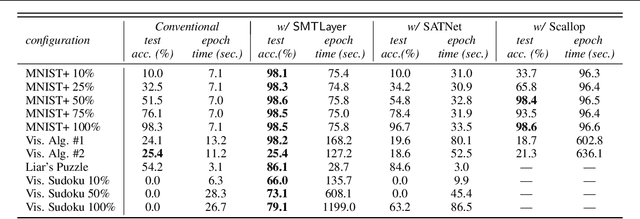
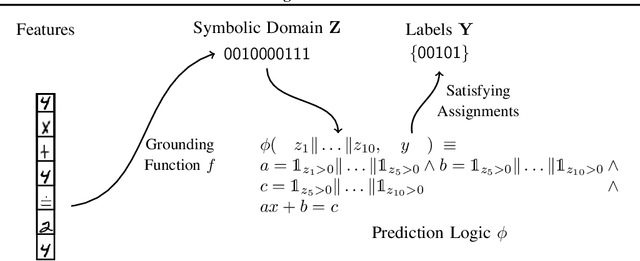
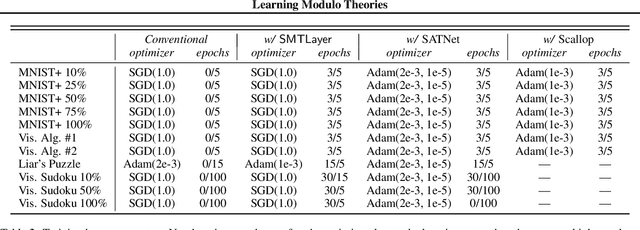
Recent techniques that integrate \emph{solver layers} into Deep Neural Networks (DNNs) have shown promise in bridging a long-standing gap between inductive learning and symbolic reasoning techniques. In this paper we present a set of techniques for integrating \emph{Satisfiability Modulo Theories} (SMT) solvers into the forward and backward passes of a deep network layer, called SMTLayer. Using this approach, one can encode rich domain knowledge into the network in the form of mathematical formulas. In the forward pass, the solver uses symbols produced by prior layers, along with these formulas, to construct inferences; in the backward pass, the solver informs updates to the network, driving it towards representations that are compatible with the solver's theory. Notably, the solver need not be differentiable. We implement \layername as a Pytorch module, and our empirical results show that it leads to models that \emph{1)} require fewer training samples than conventional models, \emph{2)} that are robust to certain types of covariate shift, and \emph{3)} that ultimately learn representations that are consistent with symbolic knowledge, and thus naturally interpretable.