The difference between memory and prediction in linear recurrent networks

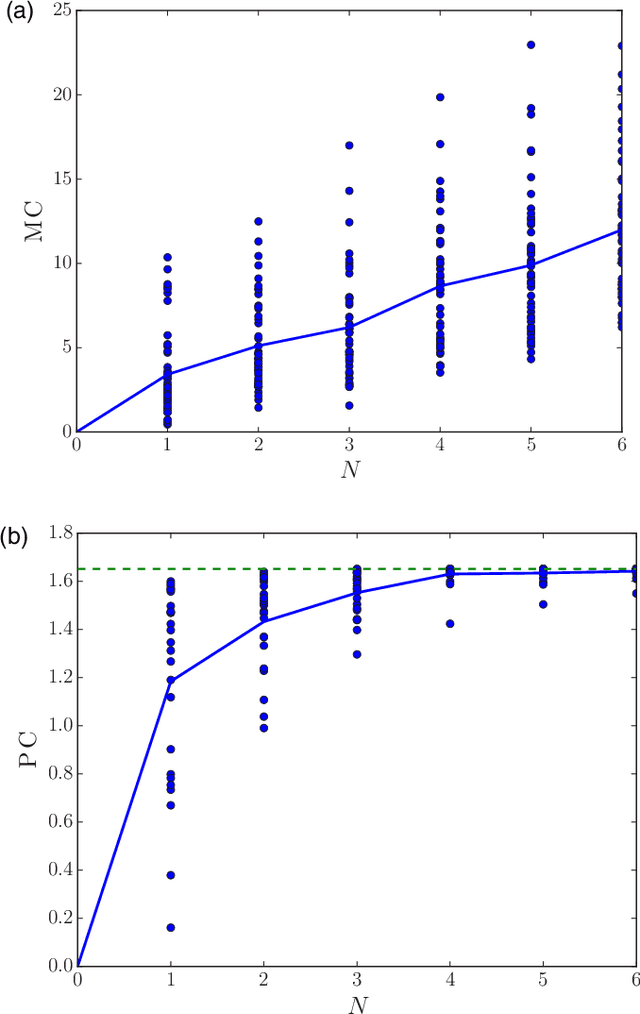
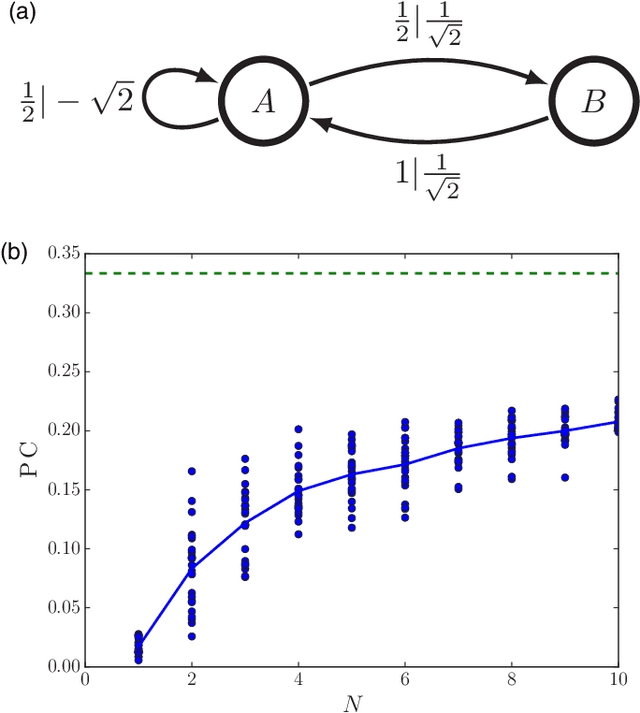
Recurrent networks are trained to memorize their input better, often in the hopes that such training will increase the ability of the network to predict. We show that networks designed to memorize input can be arbitrarily bad at prediction. We also find, for several types of inputs, that one-node networks optimized for prediction are nearly at upper bounds on predictive capacity given by Wiener filters, and are roughly equivalent in performance to randomly generated five-node networks. Our results suggest that maximizing memory capacity leads to very different networks than maximizing predictive capacity, and that optimizing recurrent weights can decrease reservoir size by half an order of magnitude.

Memory and Information Processing in Recurrent Neural Networks

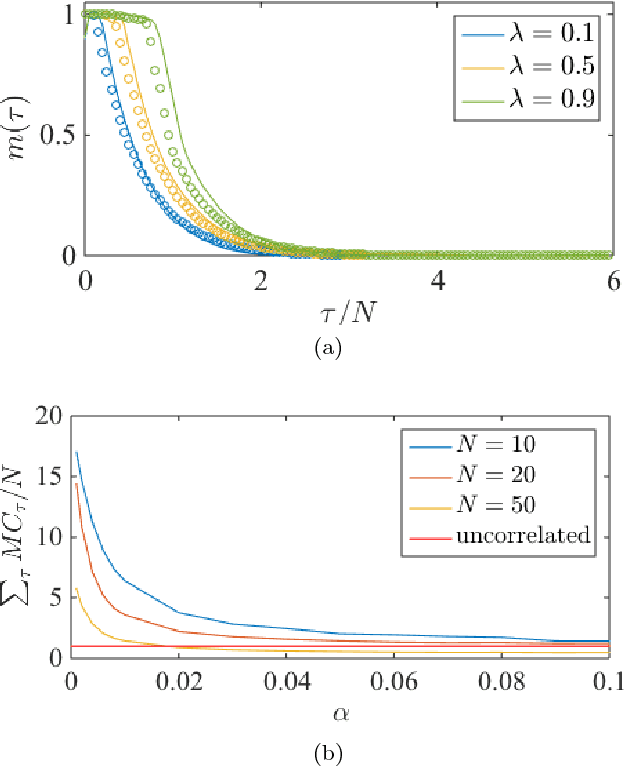
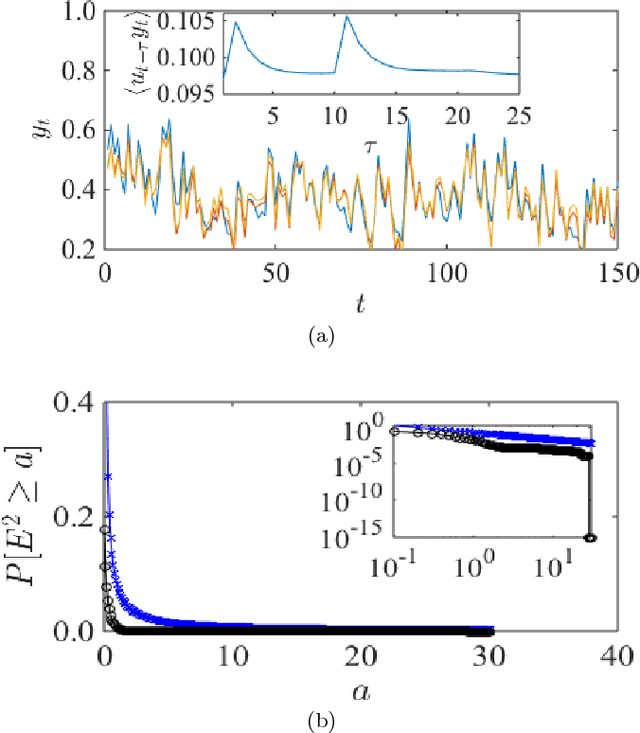
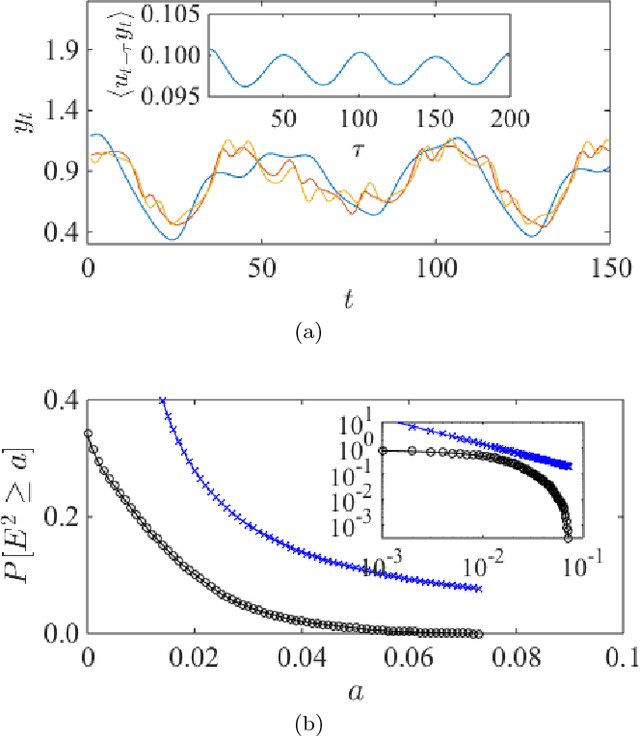
Recurrent neural networks (RNN) are simple dynamical systems whose computational power has been attributed to their short-term memory. Short-term memory of RNNs has been previously studied analytically only for the case of orthogonal networks, and only under annealed approximation, and uncorrelated input. Here for the first time, we present an exact solution to the memory capacity and the task-solving performance as a function of the structure of a given network instance, enabling direct determination of the function--structure relation in RNNs. We calculate the memory capacity for arbitrary networks with exponentially correlated input and further related it to the performance of the system on signal processing tasks in a supervised learning setup. We compute the expected error and the worst-case error bound as a function of the spectra of the network and the correlation structure of its inputs and outputs. Our results give an explanation for learning and generalization of task solving using short-term memory, which is crucial for building alternative computer architectures using physical phenomena based on the short-term memory principle.

Signatures of Infinity: Nonergodicity and Resource Scaling in Prediction, Complexity, and Learning

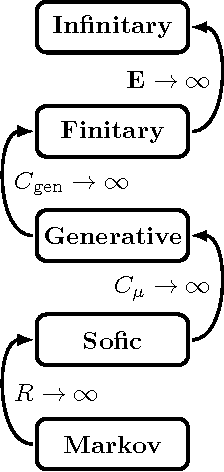
We introduce a simple analysis of the structural complexity of infinite-memory processes built from random samples of stationary, ergodic finite-memory component processes. Such processes are familiar from the well known multi-arm Bandit problem. We contrast our analysis with computation-theoretic and statistical inference approaches to understanding their complexity. The result is an alternative view of the relationship between predictability, complexity, and learning that highlights the distinct ways in which informational and correlational divergences arise in complex ergodic and nonergodic processes. We draw out consequences for the resource divergences that delineate the structural hierarchy of ergodic processes and for processes that are themselves hierarchical.

Understanding and Designing Complex Systems: Response to "A framework for optimal high-level descriptions in science and engineering---preliminary report"

We recount recent history behind building compact models of nonlinear, complex processes and identifying their relevant macroscopic patterns or "macrostates". We give a synopsis of computational mechanics, predictive rate-distortion theory, and the role of information measures in monitoring model complexity and predictive performance. Computational mechanics provides a method to extract the optimal minimal predictive model for a given process. Rate-distortion theory provides methods for systematically approximating such models. We end by commenting on future prospects for developing a general framework that automatically discovers optimal compact models. As a response to the manuscript cited in the title above, this brief commentary corrects potentially misleading claims about its state space compression method and places it in a broader historical setting.

Circumventing the Curse of Dimensionality in Prediction: Causal Rate-Distortion for Infinite-Order Markov Processes

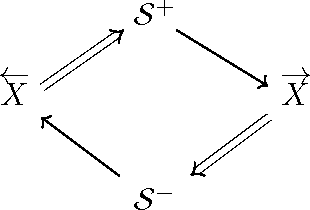
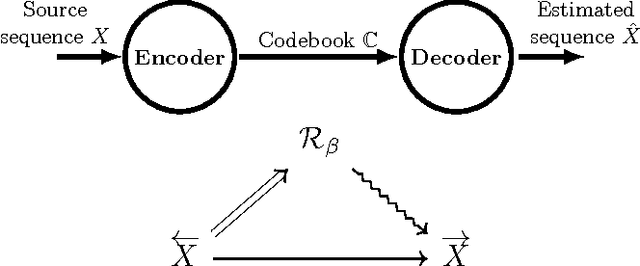
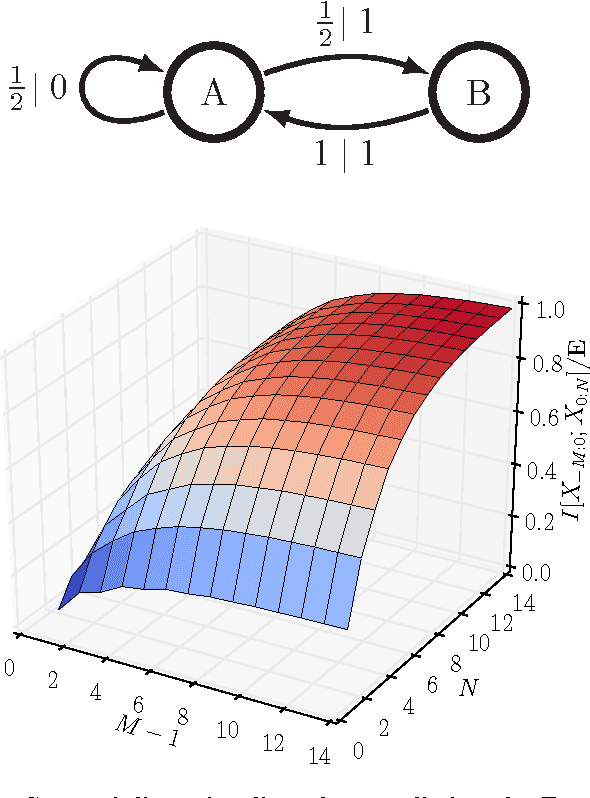
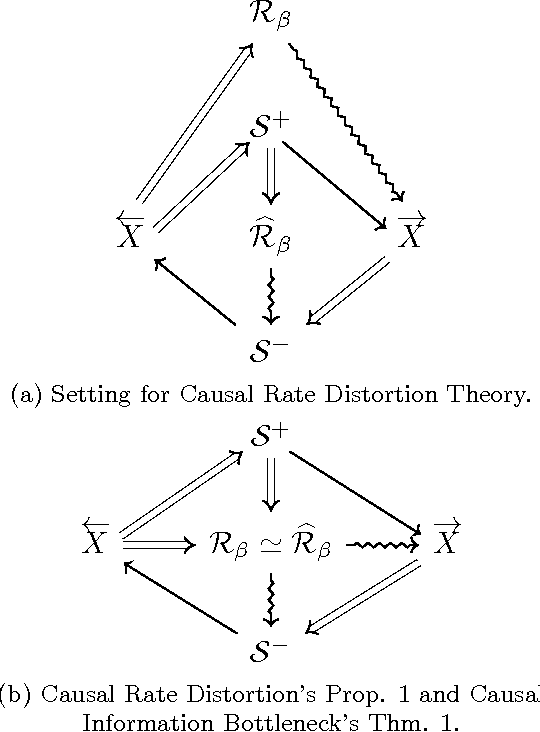
Predictive rate-distortion analysis suffers from the curse of dimensionality: clustering arbitrarily long pasts to retain information about arbitrarily long futures requires resources that typically grow exponentially with length. The challenge is compounded for infinite-order Markov processes, since conditioning on finite sequences cannot capture all of their past dependencies. Spectral arguments show that algorithms which cluster finite-length sequences fail dramatically when the underlying process has long-range temporal correlations and can fail even for processes generated by finite-memory hidden Markov models. We circumvent the curse of dimensionality in rate-distortion analysis of infinite-order processes by casting predictive rate-distortion objective functions in terms of the forward- and reverse-time causal states of computational mechanics. Examples demonstrate that the resulting causal rate-distortion theory substantially improves current predictive rate-distortion analyses.