Circumventing the Curse of Dimensionality in Prediction: Causal Rate-Distortion for Infinite-Order Markov Processes
Paper and Code
Dec 09, 2014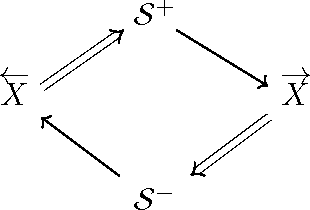
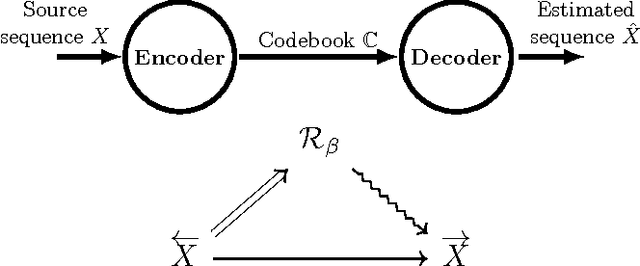
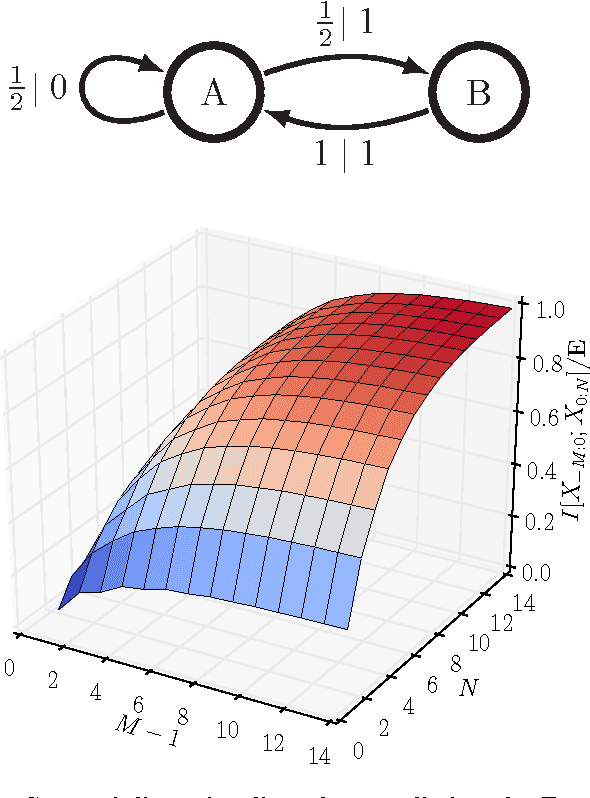
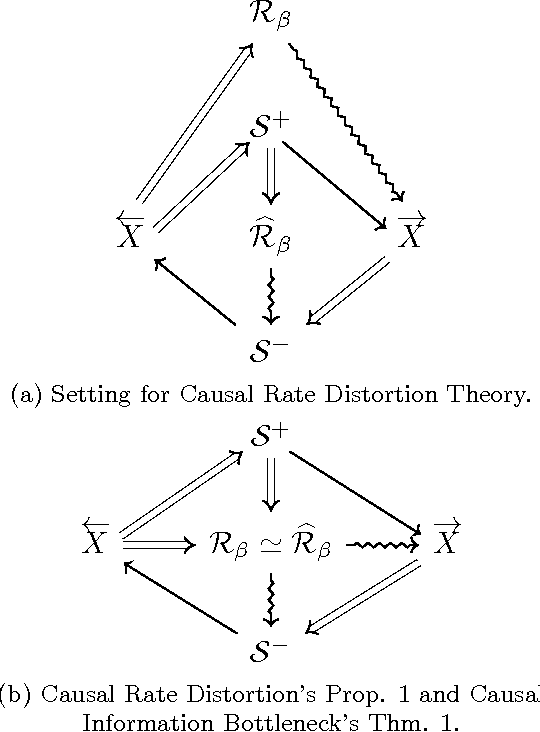
Predictive rate-distortion analysis suffers from the curse of dimensionality: clustering arbitrarily long pasts to retain information about arbitrarily long futures requires resources that typically grow exponentially with length. The challenge is compounded for infinite-order Markov processes, since conditioning on finite sequences cannot capture all of their past dependencies. Spectral arguments show that algorithms which cluster finite-length sequences fail dramatically when the underlying process has long-range temporal correlations and can fail even for processes generated by finite-memory hidden Markov models. We circumvent the curse of dimensionality in rate-distortion analysis of infinite-order processes by casting predictive rate-distortion objective functions in terms of the forward- and reverse-time causal states of computational mechanics. Examples demonstrate that the resulting causal rate-distortion theory substantially improves current predictive rate-distortion analyses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge