Unique Information via Dependency Constraints

The partial information decomposition (PID) is perhaps the leading proposal for resolving information shared between a set of sources and a target into redundant, synergistic, and unique constituents. Unfortunately, the PID framework has been hindered by a lack of a generally agreed-upon, multivariate method of quantifying the constituents. Here, we take a step toward rectifying this by developing a decomposition based on a new method that quantifies unique information. We first develop a broadly applicable method---the dependency decomposition---that delineates how statistical dependencies influence the structure of a joint distribution. The dependency decomposition then allows us to define a measure of the information about a target that can be uniquely attributed to a particular source as the least amount which the source-target statistical dependency can influence the information shared between the sources and the target. The result is the first measure that satisfies the core axioms of the PID framework while not satisfying the Blackwell relation, which depends on a particular interpretation of how the variables are related. This makes a key step forward to a practical PID.

Trimming the Independent Fat: Sufficient Statistics, Mutual Information, and Predictability from Effective Channel States

One of the most fundamental questions one can ask about a pair of random variables X and Y is the value of their mutual information. Unfortunately, this task is often stymied by the extremely large dimension of the variables. We might hope to replace each variable by a lower-dimensional representation that preserves the relationship with the other variable. The theoretically ideal implementation is the use of minimal sufficient statistics, where it is well-known that either X or Y can be replaced by their minimal sufficient statistic about the other while preserving the mutual information. While intuitively reasonable, it is not obvious or straightforward that both variables can be replaced simultaneously. We demonstrate that this is in fact possible: the information X's minimal sufficient statistic preserves about Y is exactly the information that Y's minimal sufficient statistic preserves about X. As an important corollary, we consider the case where one variable is a stochastic process' past and the other its future and the present is viewed as a memoryful channel. In this case, the mutual information is the channel transmission rate between the channel's effective states. That is, the past-future mutual information (the excess entropy) is the amount of information about the future that can be predicted using the past. Translating our result about minimal sufficient statistics, this is equivalent to the mutual information between the forward- and reverse-time causal states of computational mechanics. We close by discussing multivariate extensions to this use of minimal sufficient statistics.

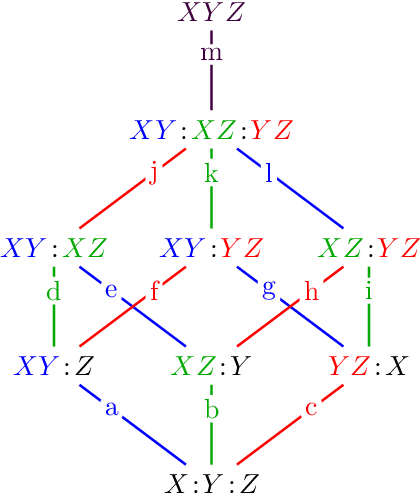
Multivariate Dependence Beyond Shannon Information

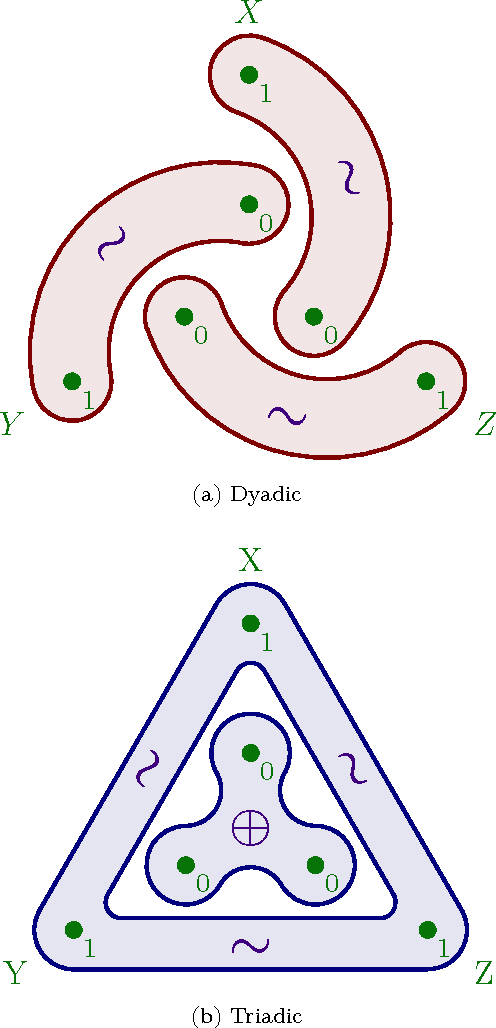
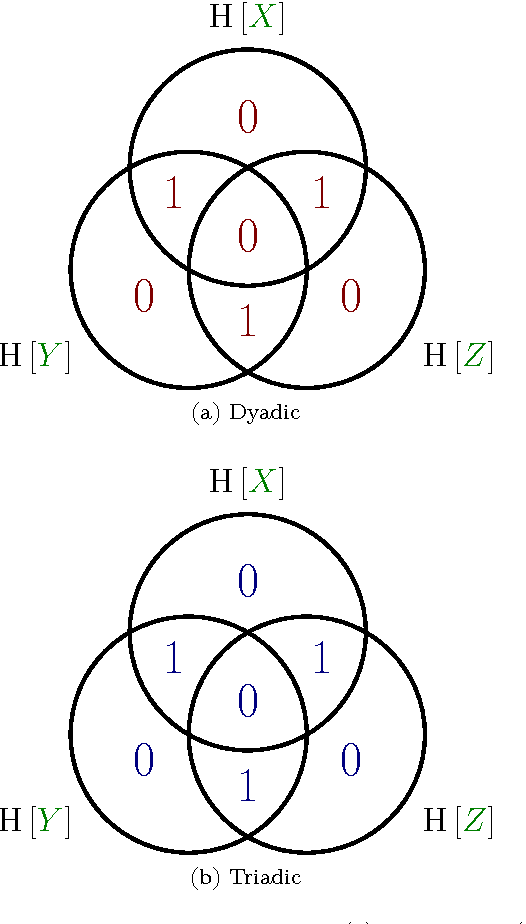
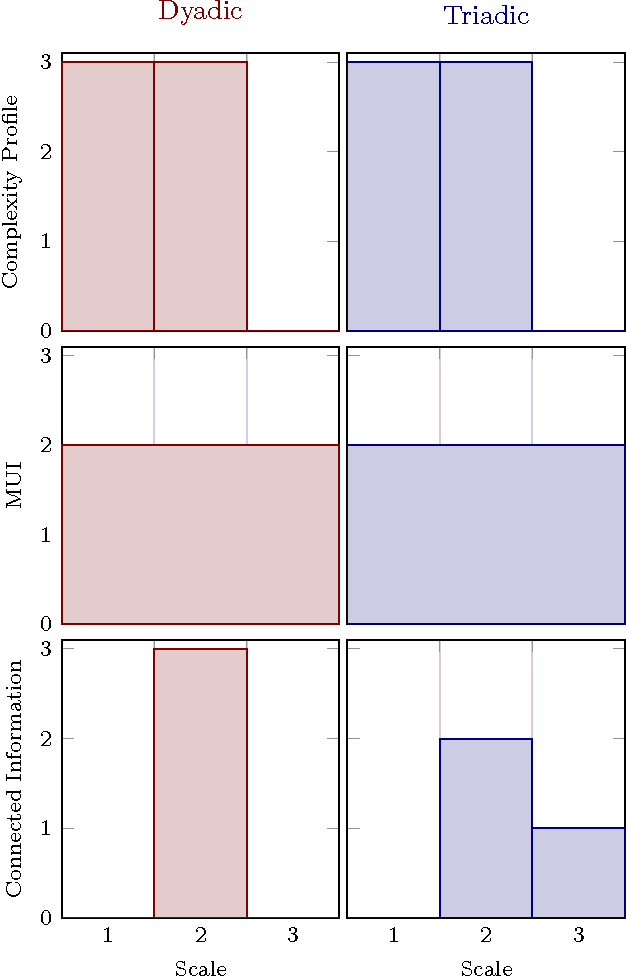
Accurately determining dependency structure is critical to discovering a system's causal organization. We recently showed that the transfer entropy fails in a key aspect of this---measuring information flow---due to its conflation of dyadic and polyadic relationships. We extend this observation to demonstrate that this is true of all such Shannon information measures when used to analyze multivariate dependencies. This has broad implications, particularly when employing information to express the organization and mechanisms embedded in complex systems, including the burgeoning efforts to combine complex network theory with information theory. Here, we do not suggest that any aspect of information theory is wrong. Rather, the vast majority of its informational measures are simply inadequate for determining the meaningful dependency structure within joint probability distributions. Therefore, such information measures are inadequate for discovering intrinsic causal relations. We close by demonstrating that such distributions exist across an arbitrary set of variables.

The Elusive Present: Hidden Past and Future Dependency and Why We Build Models

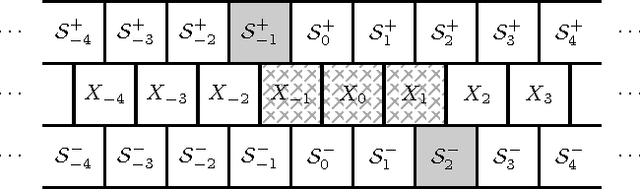
Modeling a temporal process as if it is Markovian assumes the present encodes all of the process's history. When this occurs, the present captures all of the dependency between past and future. We recently showed that if one randomly samples in the space of structured processes, this is almost never the case. So, how does the Markov failure come about? That is, how do individual measurements fail to encode the past? And, how many are needed to capture dependencies between the past and future? Here, we investigate how much information can be shared between the past and future, but not be reflected in the present. We quantify this elusive information, give explicit calculational methods, and draw out the consequences. The most important of which is that when the present hides past-future dependency we must move beyond sequence-based statistics and build state-based models.

Understanding and Designing Complex Systems: Response to "A framework for optimal high-level descriptions in science and engineering---preliminary report"

We recount recent history behind building compact models of nonlinear, complex processes and identifying their relevant macroscopic patterns or "macrostates". We give a synopsis of computational mechanics, predictive rate-distortion theory, and the role of information measures in monitoring model complexity and predictive performance. Computational mechanics provides a method to extract the optimal minimal predictive model for a given process. Rate-distortion theory provides methods for systematically approximating such models. We end by commenting on future prospects for developing a general framework that automatically discovers optimal compact models. As a response to the manuscript cited in the title above, this brief commentary corrects potentially misleading claims about its state space compression method and places it in a broader historical setting.

Synchronization and Control in Intrinsic and Designed Computation: An Information-Theoretic Analysis of Competing Models of Stochastic Computation

We adapt tools from information theory to analyze how an observer comes to synchronize with the hidden states of a finitary, stationary stochastic process. We show that synchronization is determined by both the process's internal organization and by an observer's model of it. We analyze these components using the convergence of state-block and block-state entropies, comparing them to the previously known convergence properties of the Shannon block entropy. Along the way, we introduce a hierarchy of information quantifiers as derivatives and integrals of these entropies, which parallels a similar hierarchy introduced for block entropy. We also draw out the duality between synchronization properties and a process's controllability. The tools lead to a new classification of a process's alternative representations in terms of minimality, synchronizability, and unifilarity.