Reliable Classification Explanations via Adversarial Attacks on Robust Networks

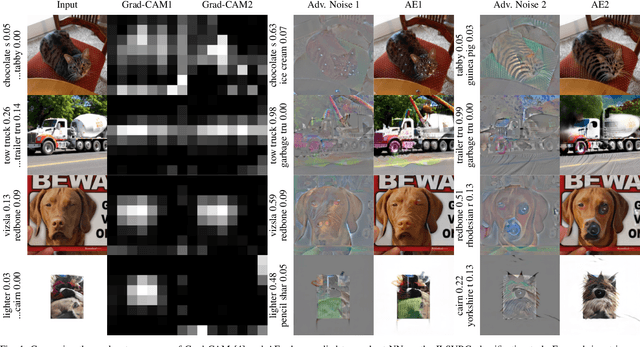
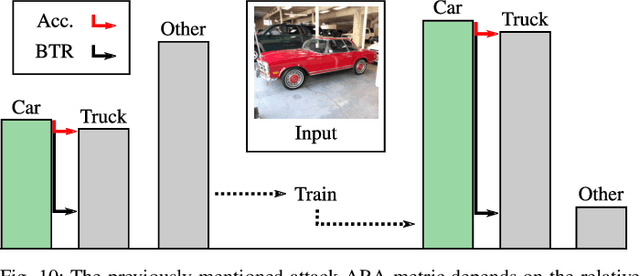
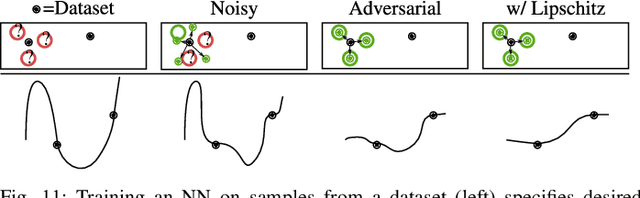
Neural Networks (NNs) have been found vulnerable to a class of imperceptible attacks, called adversarial examples, which arbitrarily alter the output of the network. These attacks have called the validity of NNs into question, particularly on sensitive problems such as medical imaging or fraud detection. We further argue that the fields of explainable AI and Human-In-The-Loop (HITL) algorithms are impacted by adversarial attacks, as attacks result in perturbations outside of the salient regions highlighted by state-of-the-art techniques such as LIME or Grad-CAM. This work accomplishes three things which greatly reduce the impact of adversarial examples, and pave the way for future HITL workflows: we propose a novel regularization technique inspired by the Lipschitz constraint which greatly improves an NN's resistance to adversarial examples; we propose a collection of novel network and training changes to complement the proposed regularization technique, including a Half-Huber activation function and an integrator-based controller for regularization strength; and we demonstrate that networks trained with this technique may be deliberately attacked to generate rich explanations. Our techniques led to networks more robust than the previous state of the art: using the Accuracy-Robustness Area (ARA), our most robust ImageNet classification network scored 42.2% top-1 accuracy on unmodified images and demonstrated an attack ARA of 0.0053, an ARA 2.4x greater than the previous state-of-the-art at the same level of accuracy on clean data, achieved with a network one-third the size. A far-reaching benefit of this technique is its ability to intuitively demonstrate decision boundaries to a human observer, allowing for improved debugging of NN decisions, and providing a means for improving the underlying model.

Memory and Information Processing in Recurrent Neural Networks

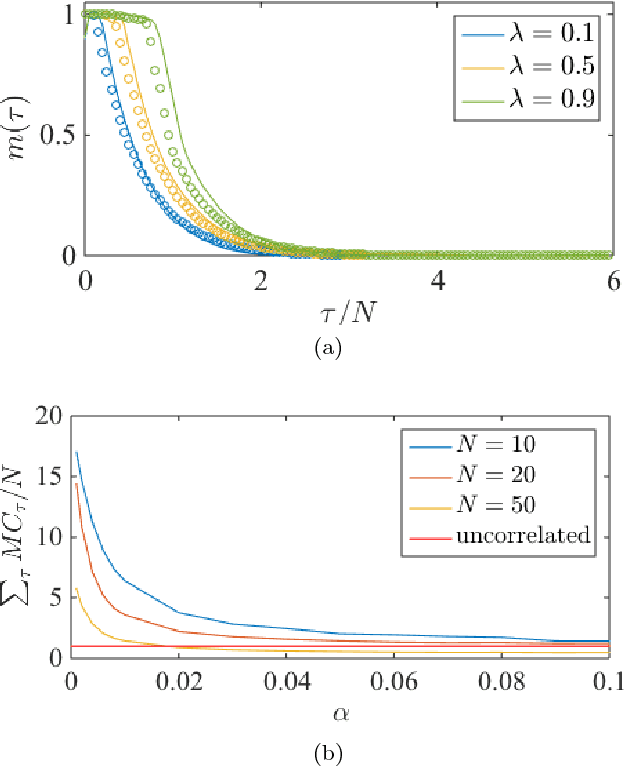
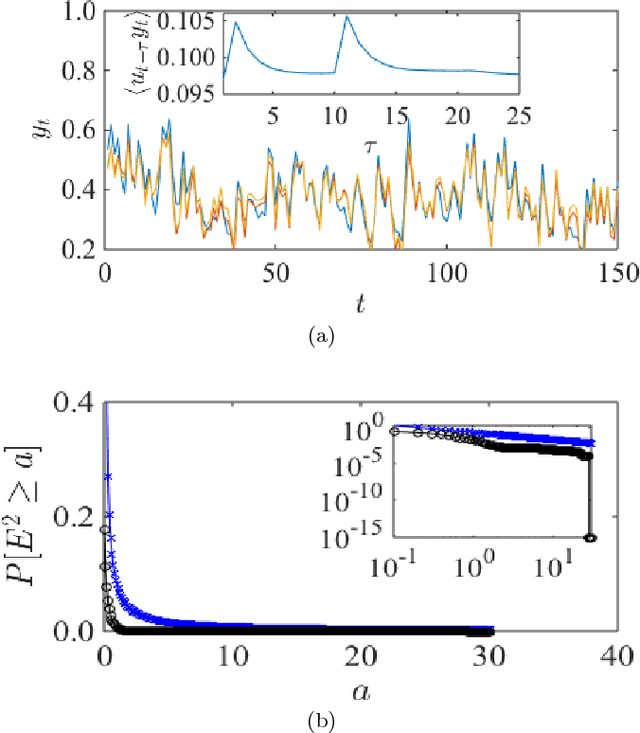
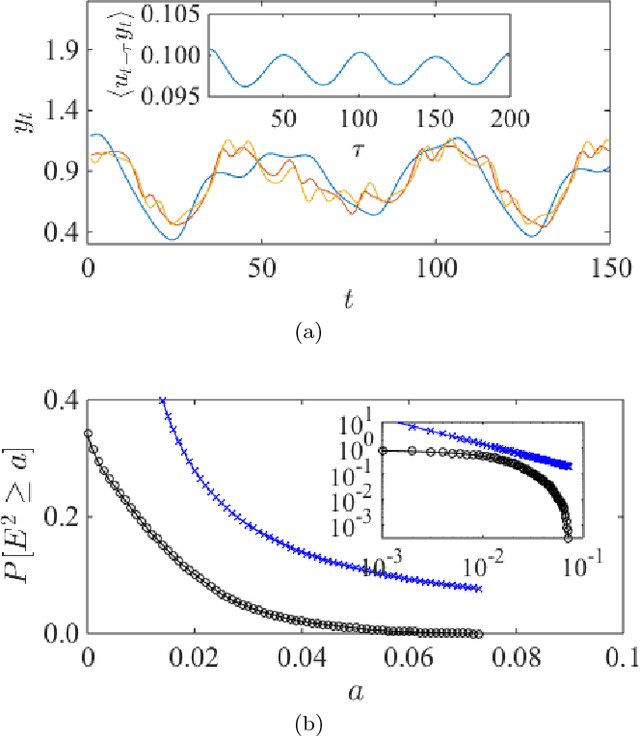
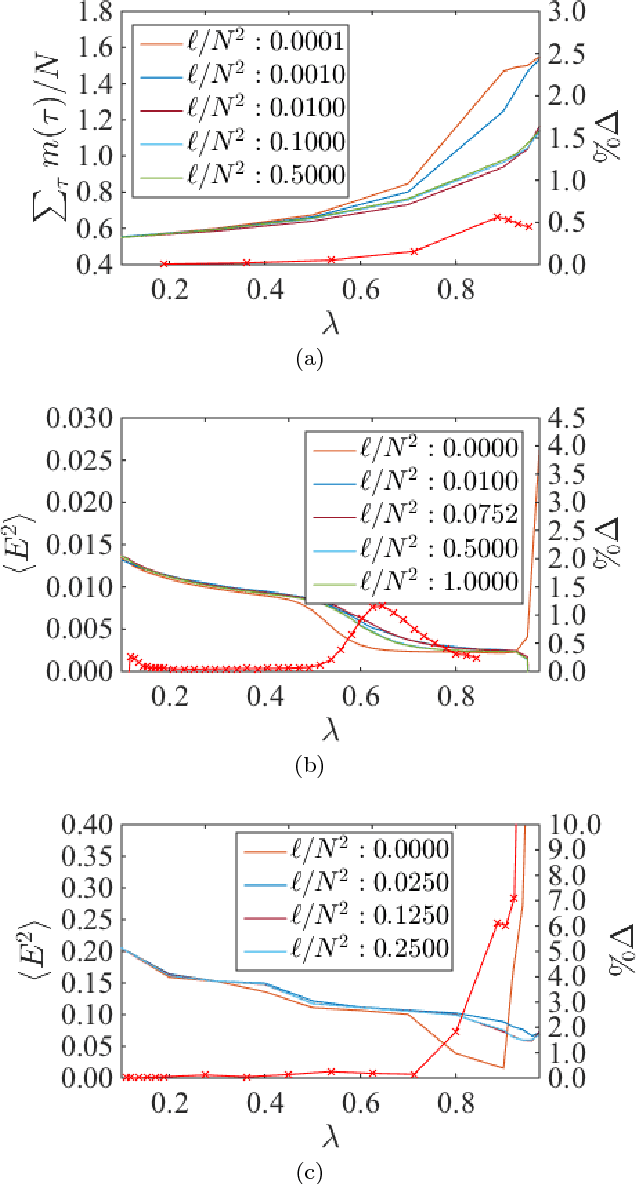
Recurrent neural networks (RNN) are simple dynamical systems whose computational power has been attributed to their short-term memory. Short-term memory of RNNs has been previously studied analytically only for the case of orthogonal networks, and only under annealed approximation, and uncorrelated input. Here for the first time, we present an exact solution to the memory capacity and the task-solving performance as a function of the structure of a given network instance, enabling direct determination of the function--structure relation in RNNs. We calculate the memory capacity for arbitrary networks with exponentially correlated input and further related it to the performance of the system on signal processing tasks in a supervised learning setup. We compute the expected error and the worst-case error bound as a function of the spectra of the network and the correlation structure of its inputs and outputs. Our results give an explanation for learning and generalization of task solving using short-term memory, which is crucial for building alternative computer architectures using physical phenomena based on the short-term memory principle.

Hierarchical Composition of Memristive Networks for Real-Time Computing

Advances in materials science have led to physical instantiations of self-assembled networks of memristive devices and demonstrations of their computational capability through reservoir computing. Reservoir computing is an approach that takes advantage of collective system dynamics for real-time computing. A dynamical system, called a reservoir, is excited with a time-varying signal and observations of its states are used to reconstruct a desired output signal. However, such a monolithic assembly limits the computational power due to signal interdependency and the resulting correlated readouts. Here, we introduce an approach that hierarchically composes a set of interconnected memristive networks into a larger reservoir. We use signal amplification and restoration to reduce reservoir state correlation, which improves the feature extraction from the input signals. Using the same number of output signals, such a hierarchical composition of heterogeneous small networks outperforms monolithic memristive networks by at least 20% on waveform generation tasks. On the NARMA-10 task, we reduce the error by up to a factor of 2 compared to homogeneous reservoirs with sigmoidal neurons, whereas single memristive networks are unable to produce the correct result. Hierarchical composition is key for solving more complex tasks with such novel nano-scale hardware.

Learning Two-input Linear and Nonlinear Analog Functions with a Simple Chemical System

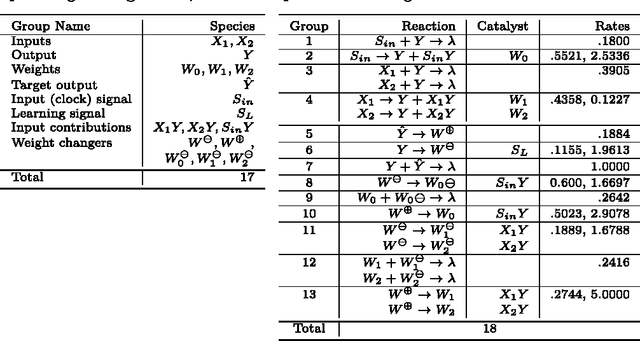
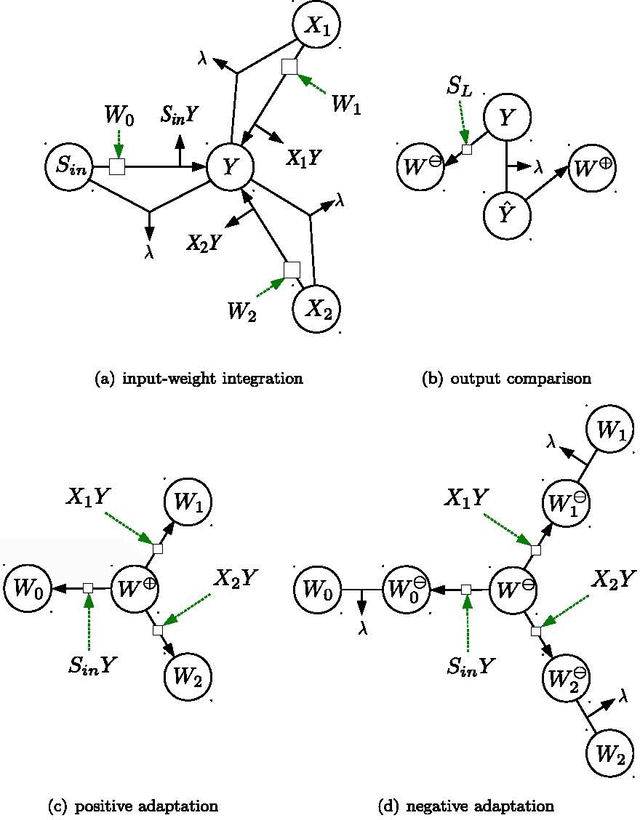
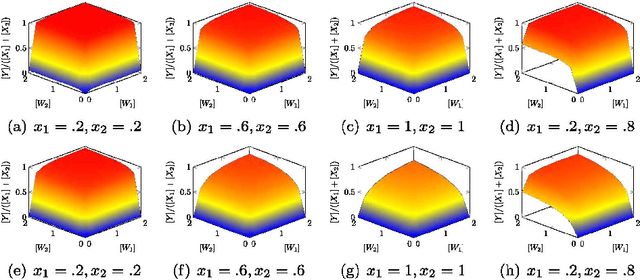
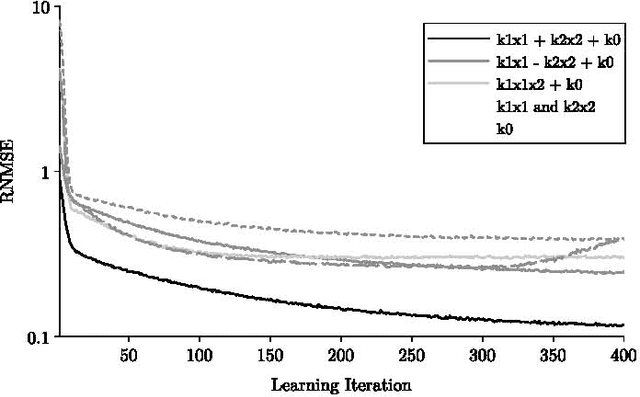
The current biochemical information processing systems behave in a predetermined manner because all features are defined during the design phase. To make such unconventional computing systems reusable and programmable for biomedical applications, adaptation, learning, and self-modification based on external stimuli would be highly desirable. However, so far, it has been too challenging to implement these in wet chemistries. In this paper we extend the chemical perceptron, a model previously proposed by the authors, to function as an analog instead of a binary system. The new analog asymmetric signal perceptron learns through feedback and supports Michaelis-Menten kinetics. The results show that our perceptron is able to learn linear and nonlinear (quadratic) functions of two inputs. To the best of our knowledge, it is the first simulated chemical system capable of doing so. The small number of species and reactions and their simplicity allows for a mapping to an actual wet implementation using DNA-strand displacement or deoxyribozymes. Our results are an important step toward actual biochemical systems that can learn and adapt.

A Comparative Study of Reservoir Computing for Temporal Signal Processing

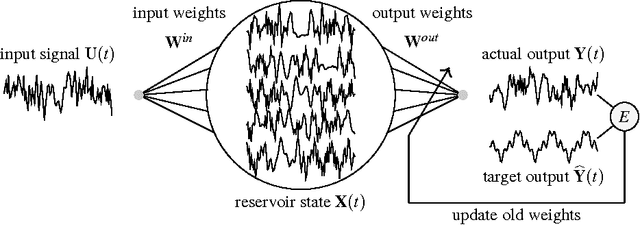
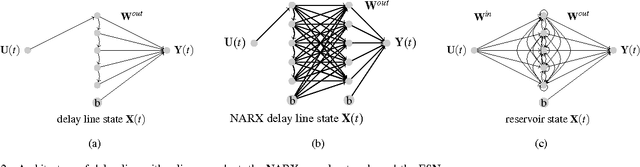
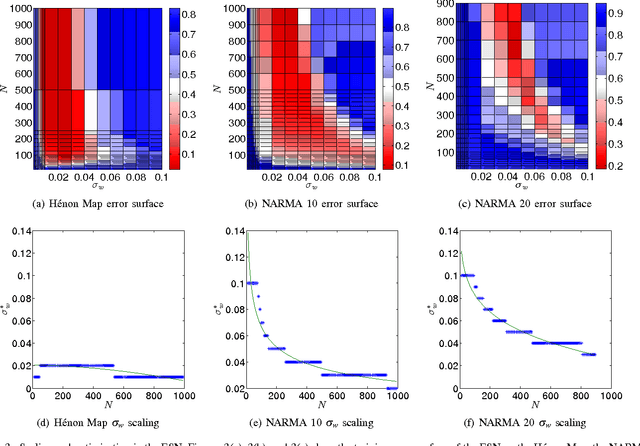
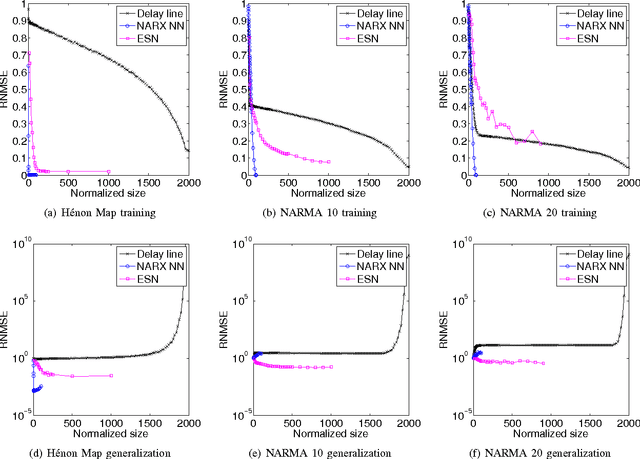
Reservoir computing (RC) is a novel approach to time series prediction using recurrent neural networks. In RC, an input signal perturbs the intrinsic dynamics of a medium called a reservoir. A readout layer is then trained to reconstruct a target output from the reservoir's state. The multitude of RC architectures and evaluation metrics poses a challenge to both practitioners and theorists who study the task-solving performance and computational power of RC. In addition, in contrast to traditional computation models, the reservoir is a dynamical system in which computation and memory are inseparable, and therefore hard to analyze. Here, we compare echo state networks (ESN), a popular RC architecture, with tapped-delay lines (DL) and nonlinear autoregressive exogenous (NARX) networks, which we use to model systems with limited computation and limited memory respectively. We compare the performance of the three systems while computing three common benchmark time series: H{\'e}non Map, NARMA10, and NARMA20. We find that the role of the reservoir in the reservoir computing paradigm goes beyond providing a memory of the past inputs. The DL and the NARX network have higher memorization capability, but fall short of the generalization power of the ESN.

Learning, Generalization, and Functional Entropy in Random Automata Networks

It has been shown \citep{broeck90:physicalreview,patarnello87:europhys} that feedforward Boolean networks can learn to perform specific simple tasks and generalize well if only a subset of the learning examples is provided for learning. Here, we extend this body of work and show experimentally that random Boolean networks (RBNs), where both the interconnections and the Boolean transfer functions are chosen at random initially, can be evolved by using a state-topology evolution to solve simple tasks. We measure the learning and generalization performance, investigate the influence of the average node connectivity $K$, the system size $N$, and introduce a new measure that allows to better describe the network's learning and generalization behavior. We show that the connectivity of the maximum entropy networks scales as a power-law of the system size $N$. Our results show that networks with higher average connectivity $K$ (supercritical) achieve higher memorization and partial generalization. However, near critical connectivity, the networks show a higher perfect generalization on the even-odd task.

Computational Capabilities of Random Automata Networks for Reservoir Computing

This paper underscores the conjecture that intrinsic computation is maximal in systems at the "edge of chaos." We study the relationship between dynamics and computational capability in Random Boolean Networks (RBN) for Reservoir Computing (RC). RC is a computational paradigm in which a trained readout layer interprets the dynamics of an excitable component (called the reservoir) that is perturbed by external input. The reservoir is often implemented as a homogeneous recurrent neural network, but there has been little investigation into the properties of reservoirs that are discrete and heterogeneous. Random Boolean networks are generic and heterogeneous dynamical systems and here we use them as the reservoir. An RBN is typically a closed system; to use it as a reservoir we extend it with an input layer. As a consequence of perturbation, the RBN does not necessarily fall into an attractor. Computational capability in RC arises from a trade-off between separability and fading memory of inputs. We find the balance of these properties predictive of classification power and optimal at critical connectivity. These results are relevant to the construction of devices which exploit the intrinsic dynamics of complex heterogeneous systems, such as biomolecular substrates.

Emergent Criticality Through Adaptive Information Processing in Boolean Networks

We study information processing in populations of Boolean networks with evolving connectivity and systematically explore the interplay between the learning capability, robustness, the network topology, and the task complexity. We solve a long-standing open question and find computationally that, for large system sizes $N$, adaptive information processing drives the networks to a critical connectivity $K_{c}=2$. For finite size networks, the connectivity approaches the critical value with a power-law of the system size $N$. We show that network learning and generalization are optimized near criticality, given task complexity and the amount of information provided threshold values. Both random and evolved networks exhibit maximal topological diversity near $K_{c}$. We hypothesize that this supports efficient exploration and robustness of solutions. Also reflected in our observation is that the variance of the values is maximal in critical network populations. Finally, we discuss implications of our results for determining the optimal topology of adaptive dynamical networks that solve computational tasks.

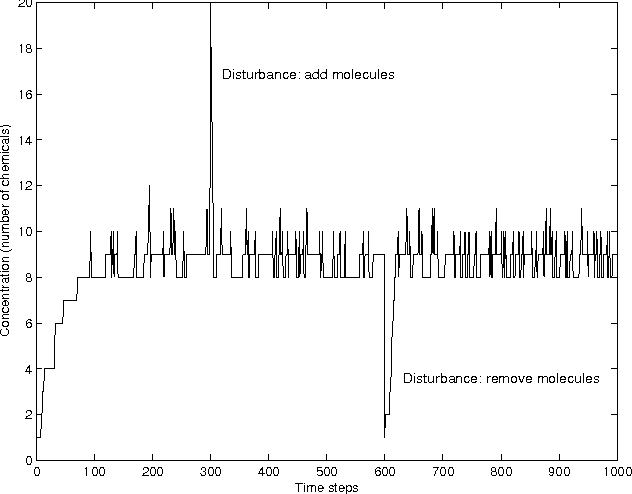
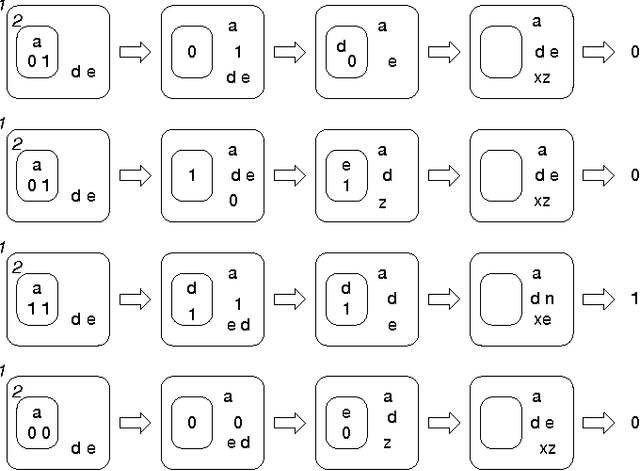
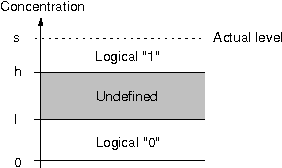
Exploring Logic Artificial Chemistries: An Illogical Attempt?

Robustness to a wide variety of negative factors and the ability to self-repair is an inherent and natural characteristic of all life forms on earth. As opposed to nature, man-made systems are in most cases not inherently robust and a significant effort has to be made in order to make them resistant against failures. This can be done in a wide variety of ways and on various system levels. In the field of digital systems, for example, techniques such as triple modular redundancy (TMR) are frequently used, which results in a considerable hardware overhead. Biologically-inspired computing by means of bio-chemical metaphors offers alternative paradigms, which need to be explored and evaluated. Here, we are interested to evaluate the potential of nature-inspired artificial chemistries and membrane systems as an alternative information representing and processing paradigm in order to obtain robust and spatially extended Boolean computing systems in a distributed environment. We investigate conceptual approaches inspired by artificial chemistries and membrane systems and compare proof-of-concepts. First, we show, that elementary logical functions can be implemented. Second, we illustrate how they can be made more robust and how they can be assembled to larger-scale systems. Finally, we discuss the implications for and paths to possible genuine implementations. Compared to the main body of work in artificial chemistries, we take a very pragmatic and implementation-oriented approach and are interested in realizing Boolean computations only. The results emphasize that artificial chemistries can be used to implement Boolean logic in a spatially extended and distributed environment and can also be made highly robust, but at a significant price.