Random active path model of deep neural networks with diluted binary synapses

Deep learning has become a powerful and popular tool for a variety of machine learning tasks. However, it is challenging to understand the mechanism of deep learning from a theoretical perspective. In this work, we propose a random active path model to study collective properties of deep neural networks with binary synapses, under the removal perturbation of connections between layers. In the model, the path from input to output is randomly activated, and the corresponding input unit constrains the weights along the path into the form of a $p$-weight interaction glass model. A critical value of the perturbation is observed to separate a spin glass regime from a paramagnetic regime, with the transition being of the first order. The paramagnetic phase is conjectured to have a poor generalization performance.

Memory and Information Processing in Recurrent Neural Networks

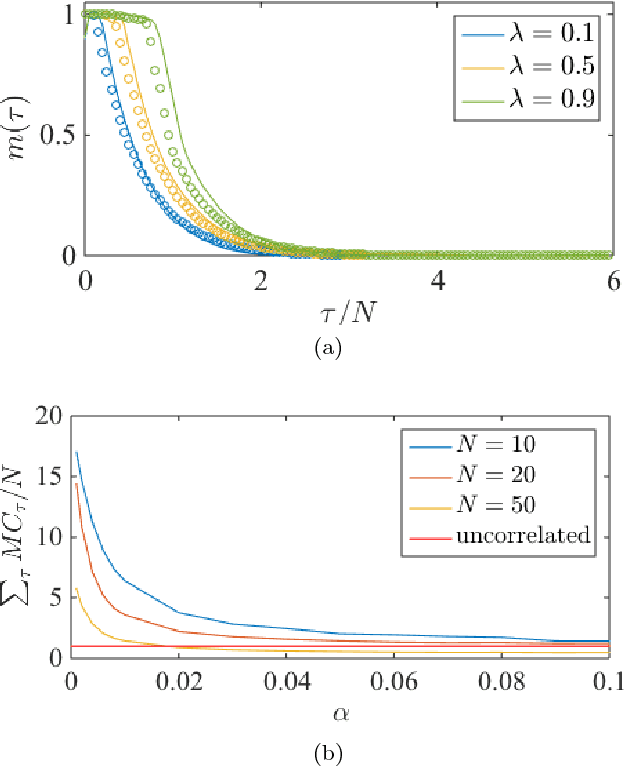
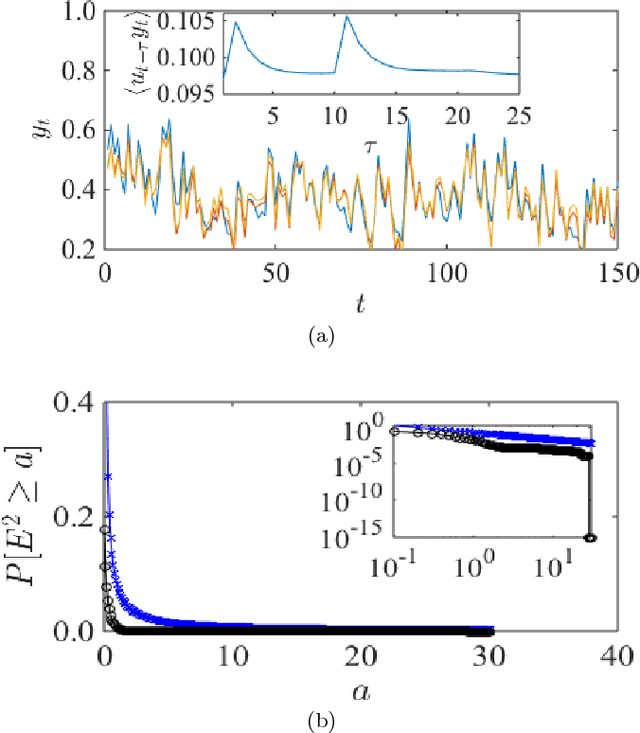
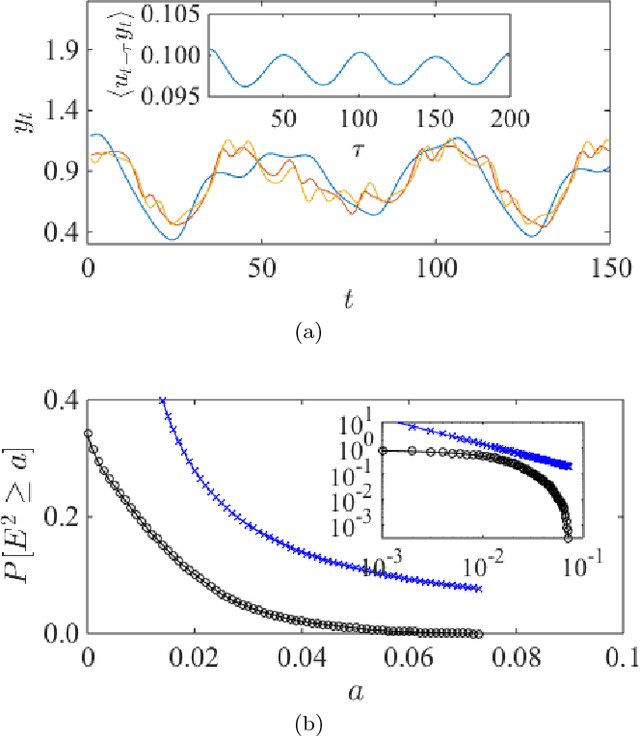
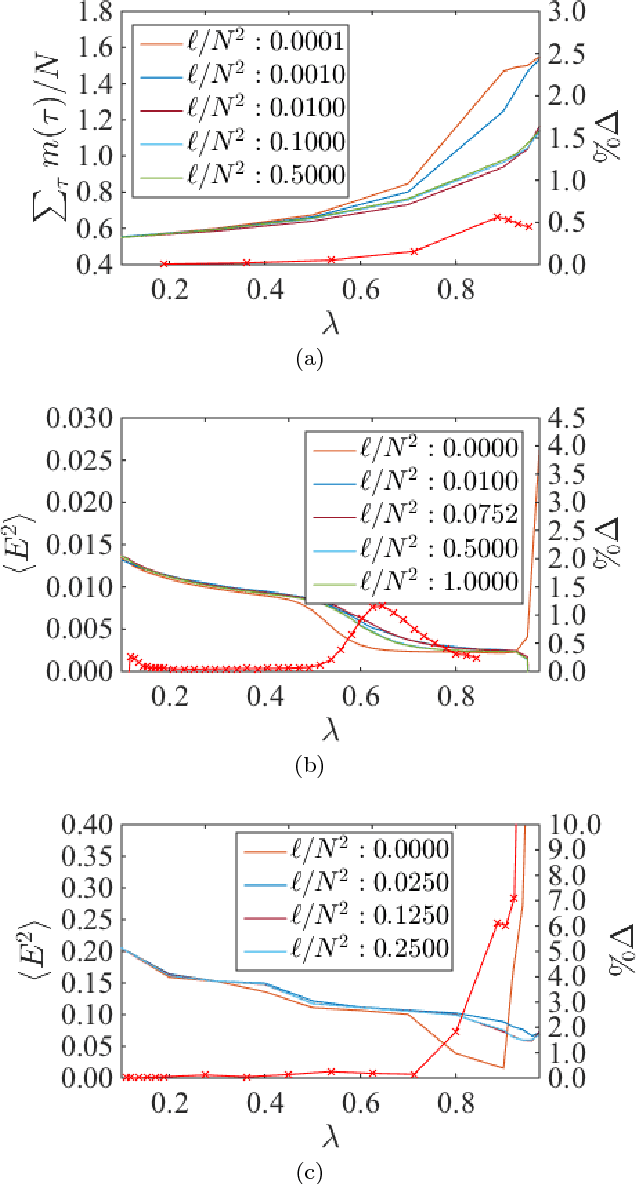
Recurrent neural networks (RNN) are simple dynamical systems whose computational power has been attributed to their short-term memory. Short-term memory of RNNs has been previously studied analytically only for the case of orthogonal networks, and only under annealed approximation, and uncorrelated input. Here for the first time, we present an exact solution to the memory capacity and the task-solving performance as a function of the structure of a given network instance, enabling direct determination of the function--structure relation in RNNs. We calculate the memory capacity for arbitrary networks with exponentially correlated input and further related it to the performance of the system on signal processing tasks in a supervised learning setup. We compute the expected error and the worst-case error bound as a function of the spectra of the network and the correlation structure of its inputs and outputs. Our results give an explanation for learning and generalization of task solving using short-term memory, which is crucial for building alternative computer architectures using physical phenomena based on the short-term memory principle.

Exploring Transfer Function Nonlinearity in Echo State Networks

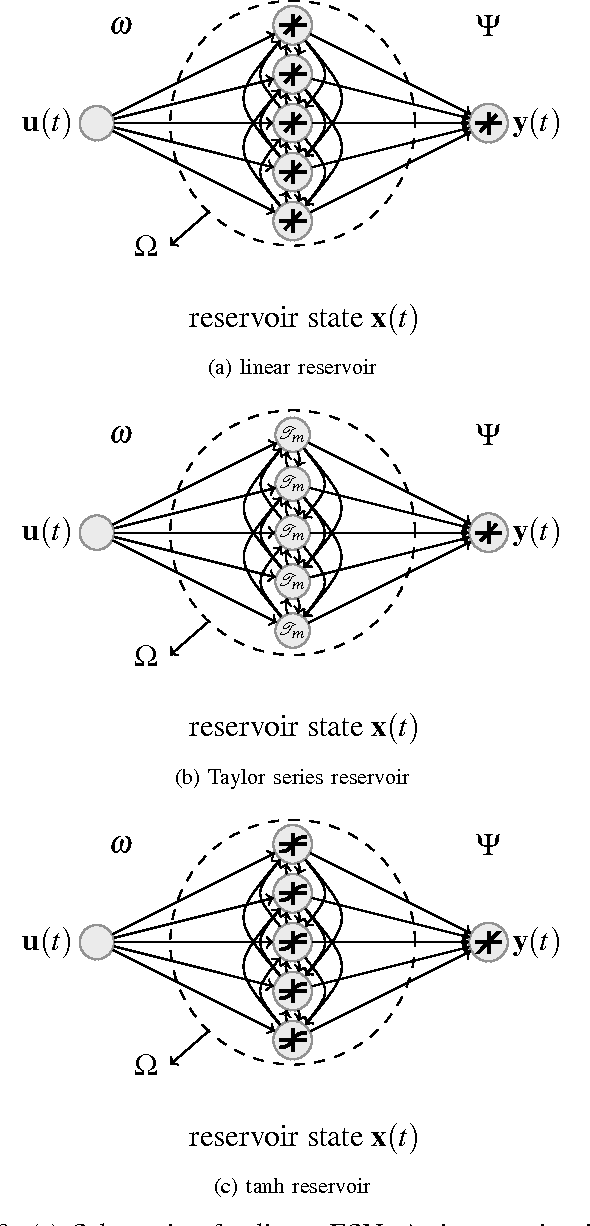
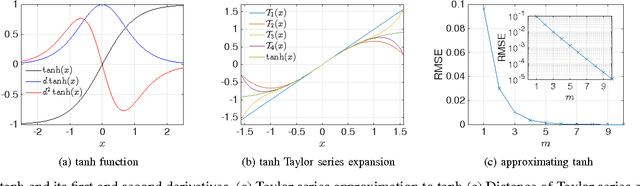
Supralinear and sublinear pre-synaptic and dendritic integration is considered to be responsible for nonlinear computation power of biological neurons, emphasizing the role of nonlinear integration as opposed to nonlinear output thresholding. How, why, and to what degree the transfer function nonlinearity helps biologically inspired neural network models is not fully understood. Here, we study these questions in the context of echo state networks (ESN). ESN is a simple neural network architecture in which a fixed recurrent network is driven with an input signal, and the output is generated by a readout layer from the measurements of the network states. ESN architecture enjoys efficient training and good performance on certain signal-processing tasks, such as system identification and time series prediction. ESN performance has been analyzed with respect to the connectivity pattern in the network structure and the input bias. However, the effects of the transfer function in the network have not been studied systematically. Here, we use an approach tanh on the Taylor expansion of a frequently used transfer function, the hyperbolic tangent function, to systematically study the effect of increasing nonlinearity of the transfer function on the memory, nonlinear capacity, and signal processing performance of ESN. Interestingly, we find that a quadratic approximation is enough to capture the computational power of ESN with tanh function. The results of this study apply to both software and hardware implementation of ESN.

Hierarchical Composition of Memristive Networks for Real-Time Computing

Advances in materials science have led to physical instantiations of self-assembled networks of memristive devices and demonstrations of their computational capability through reservoir computing. Reservoir computing is an approach that takes advantage of collective system dynamics for real-time computing. A dynamical system, called a reservoir, is excited with a time-varying signal and observations of its states are used to reconstruct a desired output signal. However, such a monolithic assembly limits the computational power due to signal interdependency and the resulting correlated readouts. Here, we introduce an approach that hierarchically composes a set of interconnected memristive networks into a larger reservoir. We use signal amplification and restoration to reduce reservoir state correlation, which improves the feature extraction from the input signals. Using the same number of output signals, such a hierarchical composition of heterogeneous small networks outperforms monolithic memristive networks by at least 20% on waveform generation tasks. On the NARMA-10 task, we reduce the error by up to a factor of 2 compared to homogeneous reservoirs with sigmoidal neurons, whereas single memristive networks are unable to produce the correct result. Hierarchical composition is key for solving more complex tasks with such novel nano-scale hardware.

Product Reservoir Computing: Time-Series Computation with Multiplicative Neurons

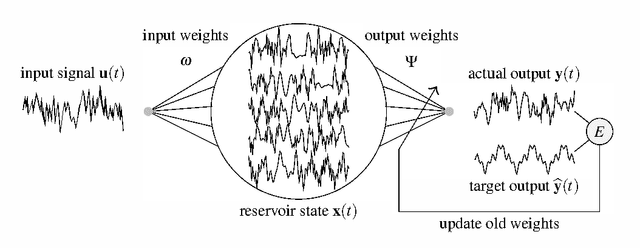
Echo state networks (ESN), a type of reservoir computing (RC) architecture, are efficient and accurate artificial neural systems for time series processing and learning. An ESN consists of a core of recurrent neural networks, called a reservoir, with a small number of tunable parameters to generate a high-dimensional representation of an input, and a readout layer which is easily trained using regression to produce a desired output from the reservoir states. Certain computational tasks involve real-time calculation of high-order time correlations, which requires nonlinear transformation either in the reservoir or the readout layer. Traditional ESN employs a reservoir with sigmoid or tanh function neurons. In contrast, some types of biological neurons obey response curves that can be described as a product unit rather than a sum and threshold. Inspired by this class of neurons, we introduce a RC architecture with a reservoir of product nodes for time series computation. We find that the product RC shows many properties of standard ESN such as short-term memory and nonlinear capacity. On standard benchmarks for chaotic prediction tasks, the product RC maintains the performance of a standard nonlinear ESN while being more amenable to mathematical analysis. Our study provides evidence that such networks are powerful in highly nonlinear tasks owing to high-order statistics generated by the recurrent product node reservoir.

Towards a Calculus of Echo State Networks

Reservoir computing is a recent trend in neural networks which uses the dynamical perturbations on the phase space of a system to compute a desired target function. We present how one can formulate an expectation of system performance in a simple class of reservoir computing called echo state networks. In contrast with previous theoretical frameworks, which only reveal an upper bound on the total memory in the system, we analytically calculate the entire memory curve as a function of the structure of the system and the properties of the input and the target function. We demonstrate the precision of our framework by validating its result for a wide range of system sizes and spectral radii. Our analytical calculation agrees with numerical simulations. To the best of our knowledge this work presents the first exact analytical characterization of the memory curve in echo state networks.

A Comparative Study of Reservoir Computing for Temporal Signal Processing

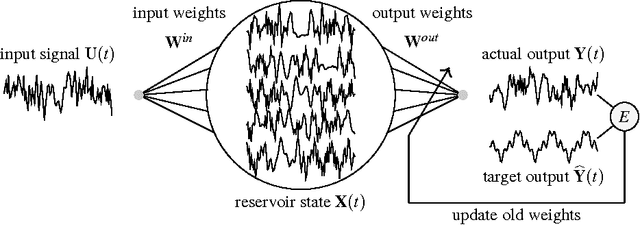
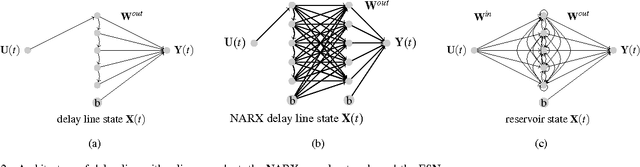
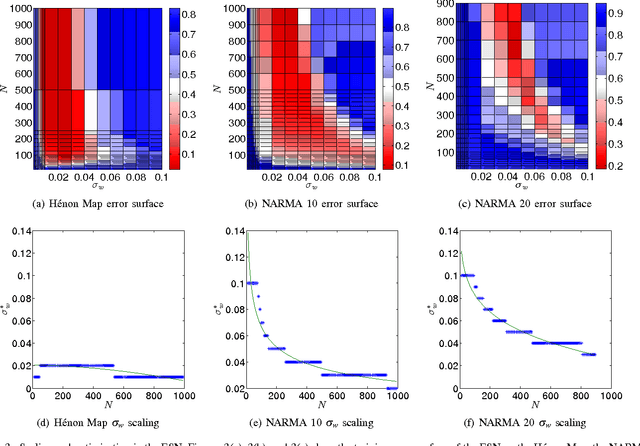
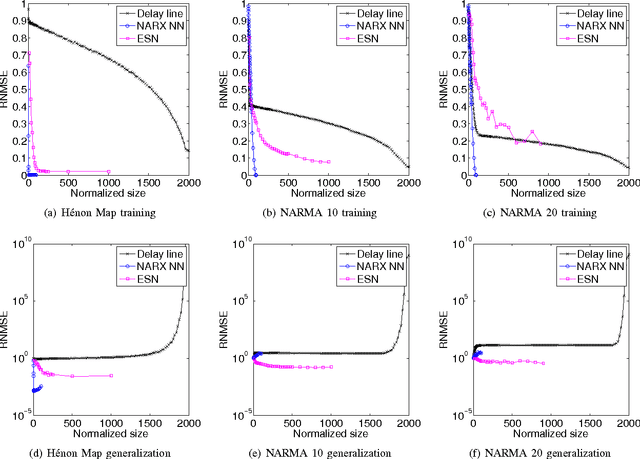
Reservoir computing (RC) is a novel approach to time series prediction using recurrent neural networks. In RC, an input signal perturbs the intrinsic dynamics of a medium called a reservoir. A readout layer is then trained to reconstruct a target output from the reservoir's state. The multitude of RC architectures and evaluation metrics poses a challenge to both practitioners and theorists who study the task-solving performance and computational power of RC. In addition, in contrast to traditional computation models, the reservoir is a dynamical system in which computation and memory are inseparable, and therefore hard to analyze. Here, we compare echo state networks (ESN), a popular RC architecture, with tapped-delay lines (DL) and nonlinear autoregressive exogenous (NARX) networks, which we use to model systems with limited computation and limited memory respectively. We compare the performance of the three systems while computing three common benchmark time series: H{\'e}non Map, NARMA10, and NARMA20. We find that the role of the reservoir in the reservoir computing paradigm goes beyond providing a memory of the past inputs. The DL and the NARX network have higher memorization capability, but fall short of the generalization power of the ESN.

Learning, Generalization, and Functional Entropy in Random Automata Networks

It has been shown \citep{broeck90:physicalreview,patarnello87:europhys} that feedforward Boolean networks can learn to perform specific simple tasks and generalize well if only a subset of the learning examples is provided for learning. Here, we extend this body of work and show experimentally that random Boolean networks (RBNs), where both the interconnections and the Boolean transfer functions are chosen at random initially, can be evolved by using a state-topology evolution to solve simple tasks. We measure the learning and generalization performance, investigate the influence of the average node connectivity $K$, the system size $N$, and introduce a new measure that allows to better describe the network's learning and generalization behavior. We show that the connectivity of the maximum entropy networks scales as a power-law of the system size $N$. Our results show that networks with higher average connectivity $K$ (supercritical) achieve higher memorization and partial generalization. However, near critical connectivity, the networks show a higher perfect generalization on the even-odd task.

DNA Reservoir Computing: A Novel Molecular Computing Approach

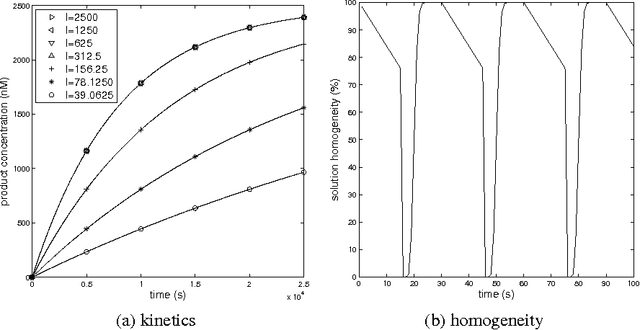
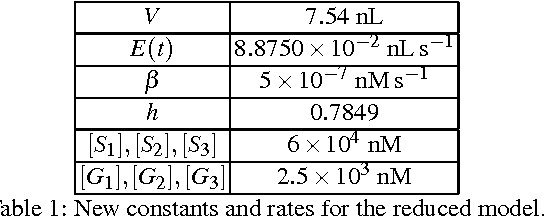
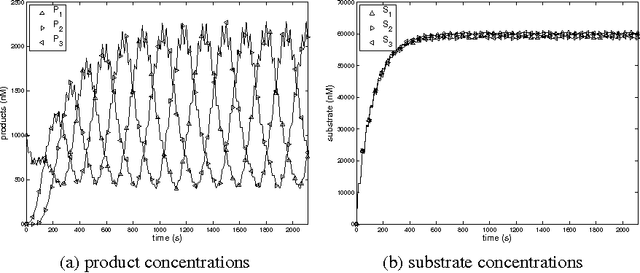
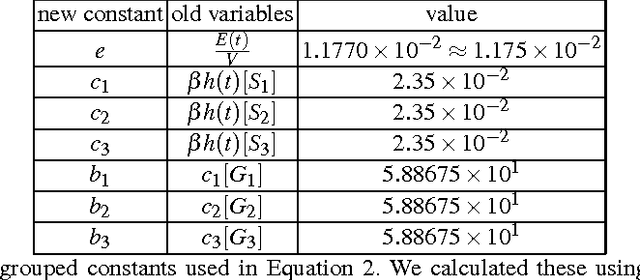
We propose a novel molecular computing approach based on reservoir computing. In reservoir computing, a dynamical core, called a reservoir, is perturbed with an external input signal while a readout layer maps the reservoir dynamics to a target output. Computation takes place as a transformation from the input space to a high-dimensional spatiotemporal feature space created by the transient dynamics of the reservoir. The readout layer then combines these features to produce the target output. We show that coupled deoxyribozyme oscillators can act as the reservoir. We show that despite using only three coupled oscillators, a molecular reservoir computer could achieve 90% accuracy on a benchmark temporal problem.

Computational Capabilities of Random Automata Networks for Reservoir Computing

This paper underscores the conjecture that intrinsic computation is maximal in systems at the "edge of chaos." We study the relationship between dynamics and computational capability in Random Boolean Networks (RBN) for Reservoir Computing (RC). RC is a computational paradigm in which a trained readout layer interprets the dynamics of an excitable component (called the reservoir) that is perturbed by external input. The reservoir is often implemented as a homogeneous recurrent neural network, but there has been little investigation into the properties of reservoirs that are discrete and heterogeneous. Random Boolean networks are generic and heterogeneous dynamical systems and here we use them as the reservoir. An RBN is typically a closed system; to use it as a reservoir we extend it with an input layer. As a consequence of perturbation, the RBN does not necessarily fall into an attractor. Computational capability in RC arises from a trade-off between separability and fading memory of inputs. We find the balance of these properties predictive of classification power and optimal at critical connectivity. These results are relevant to the construction of devices which exploit the intrinsic dynamics of complex heterogeneous systems, such as biomolecular substrates.