Quantum Autoencoders for Learning Quantum Channel Codes

This work investigates the application of quantum machine learning techniques for classical and quantum communication across different qubit channel models. By employing parameterized quantum circuits and a flexible channel noise model, we develop a machine learning framework to generate quantum channel codes and evaluate their effectiveness. We explore classical, entanglement-assisted, and quantum communication scenarios within our framework. Applying it to various quantum channel models as proof of concept, we demonstrate strong performance in each case. Our results highlight the potential of quantum machine learning in advancing research on quantum communication systems, enabling a better understanding of capacity bounds under modulation constraints, various communication settings, and diverse channel models.

Exploring Transfer Function Nonlinearity in Echo State Networks

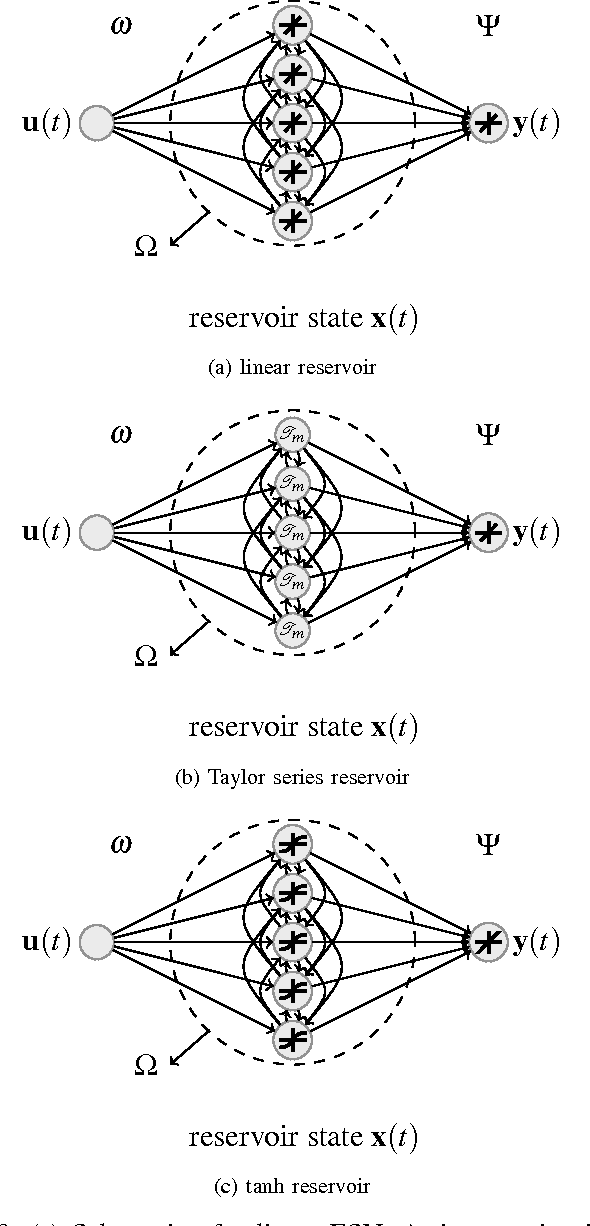
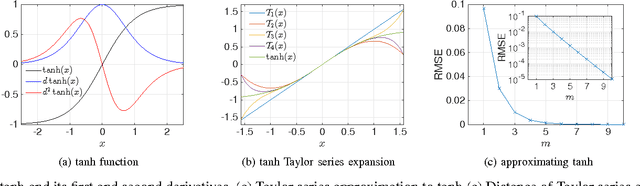
Supralinear and sublinear pre-synaptic and dendritic integration is considered to be responsible for nonlinear computation power of biological neurons, emphasizing the role of nonlinear integration as opposed to nonlinear output thresholding. How, why, and to what degree the transfer function nonlinearity helps biologically inspired neural network models is not fully understood. Here, we study these questions in the context of echo state networks (ESN). ESN is a simple neural network architecture in which a fixed recurrent network is driven with an input signal, and the output is generated by a readout layer from the measurements of the network states. ESN architecture enjoys efficient training and good performance on certain signal-processing tasks, such as system identification and time series prediction. ESN performance has been analyzed with respect to the connectivity pattern in the network structure and the input bias. However, the effects of the transfer function in the network have not been studied systematically. Here, we use an approach tanh on the Taylor expansion of a frequently used transfer function, the hyperbolic tangent function, to systematically study the effect of increasing nonlinearity of the transfer function on the memory, nonlinear capacity, and signal processing performance of ESN. Interestingly, we find that a quadratic approximation is enough to capture the computational power of ESN with tanh function. The results of this study apply to both software and hardware implementation of ESN.

Product Reservoir Computing: Time-Series Computation with Multiplicative Neurons

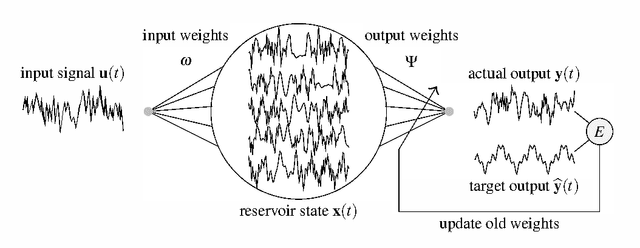
Echo state networks (ESN), a type of reservoir computing (RC) architecture, are efficient and accurate artificial neural systems for time series processing and learning. An ESN consists of a core of recurrent neural networks, called a reservoir, with a small number of tunable parameters to generate a high-dimensional representation of an input, and a readout layer which is easily trained using regression to produce a desired output from the reservoir states. Certain computational tasks involve real-time calculation of high-order time correlations, which requires nonlinear transformation either in the reservoir or the readout layer. Traditional ESN employs a reservoir with sigmoid or tanh function neurons. In contrast, some types of biological neurons obey response curves that can be described as a product unit rather than a sum and threshold. Inspired by this class of neurons, we introduce a RC architecture with a reservoir of product nodes for time series computation. We find that the product RC shows many properties of standard ESN such as short-term memory and nonlinear capacity. On standard benchmarks for chaotic prediction tasks, the product RC maintains the performance of a standard nonlinear ESN while being more amenable to mathematical analysis. Our study provides evidence that such networks are powerful in highly nonlinear tasks owing to high-order statistics generated by the recurrent product node reservoir.