Signatures of Infinity: Nonergodicity and Resource Scaling in Prediction, Complexity, and Learning
Paper and Code
Apr 01, 2015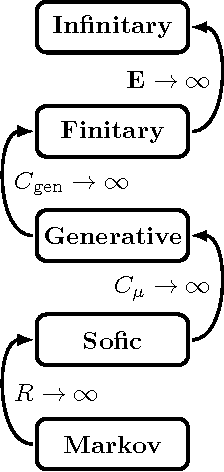
We introduce a simple analysis of the structural complexity of infinite-memory processes built from random samples of stationary, ergodic finite-memory component processes. Such processes are familiar from the well known multi-arm Bandit problem. We contrast our analysis with computation-theoretic and statistical inference approaches to understanding their complexity. The result is an alternative view of the relationship between predictability, complexity, and learning that highlights the distinct ways in which informational and correlational divergences arise in complex ergodic and nonergodic processes. We draw out consequences for the resource divergences that delineate the structural hierarchy of ergodic processes and for processes that are themselves hierarchical.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge