Efficient Hierarchical Bayesian Inference for Spatio-temporal Regression Models in Neuroimaging

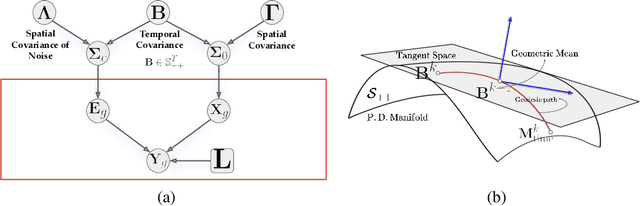
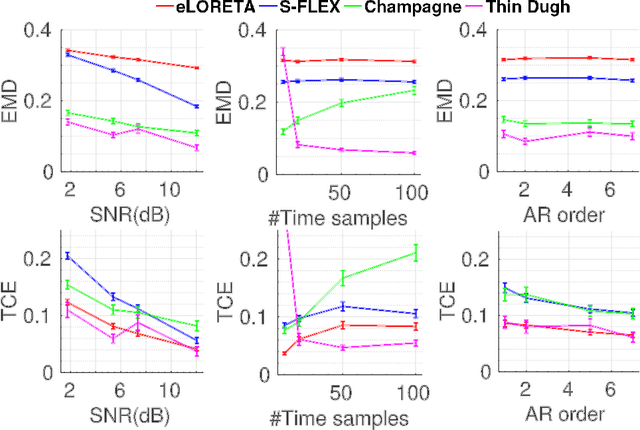
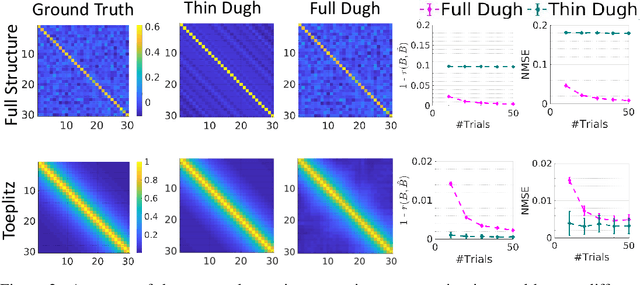
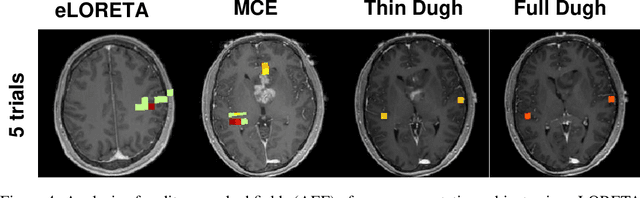
Several problems in neuroimaging and beyond require inference on the parameters of multi-task sparse hierarchical regression models. Examples include M/EEG inverse problems, neural encoding models for task-based fMRI analyses, and climate science. In these domains, both the model parameters to be inferred and the measurement noise may exhibit a complex spatio-temporal structure. Existing work either neglects the temporal structure or leads to computationally demanding inference schemes. Overcoming these limitations, we devise a novel flexible hierarchical Bayesian framework within which the spatio-temporal dynamics of model parameters and noise are modeled to have Kronecker product covariance structure. Inference in our framework is based on majorization-minimization optimization and has guaranteed convergence properties. Our highly efficient algorithms exploit the intrinsic Riemannian geometry of temporal autocovariance matrices. For stationary dynamics described by Toeplitz matrices, the theory of circulant embeddings is employed. We prove convex bounding properties and derive update rules of the resulting algorithms. On both synthetic and real neural data from M/EEG, we demonstrate that our methods lead to improved performance.

Nonlocal Co-occurrence for Image Downscaling

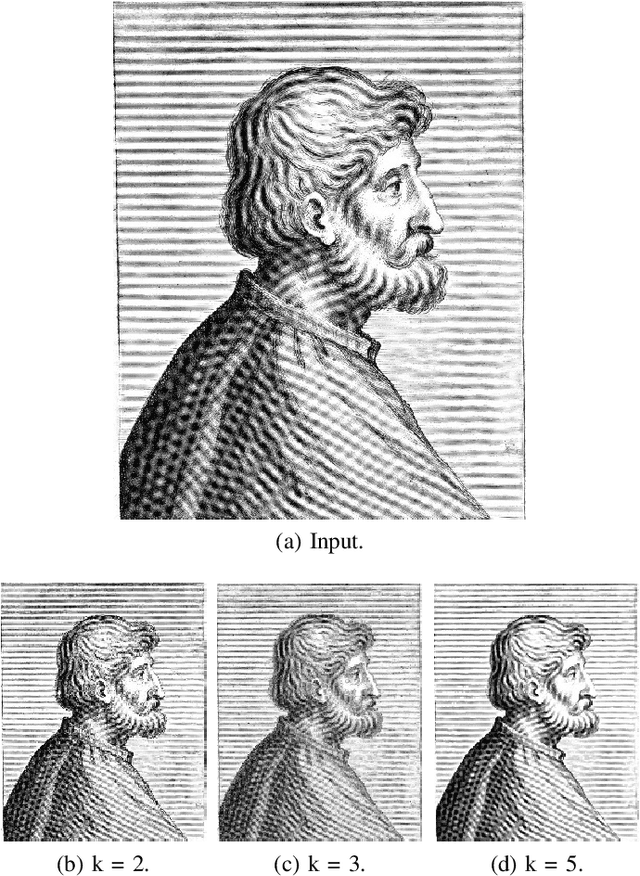
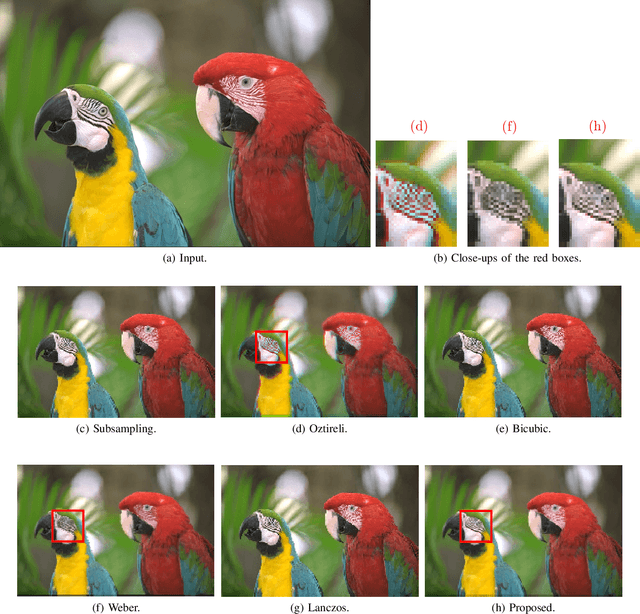
Image downscaling is one of the widely used operations in image processing and computer graphics. It was recently demonstrated in the literature that kernel-based convolutional filters could be modified to develop efficient image downscaling algorithms. In this work, we present a new downscaling technique which is based on kernel-based image filtering concept. We propose to use pairwise co-occurrence similarity of the pixelpairs as the range kernel similarity in the filtering operation. The co-occurrence of the pixel-pair is learned directly from the input image. This co-occurrence learning is performed in a neighborhood based fashion all over the image. The proposed method can preserve the high-frequency structures, which were present in the input image, into the downscaled image. The resulting images retain visually important details and do not suffer from edge-blurring artifact. We demonstrate the effectiveness of our proposed approach with extensive experiments on a large number of images downscaled with various downscaling factors.

Linearized ADMM and Fast Nonlocal Denoising for Efficient Plug-and-Play Restoration

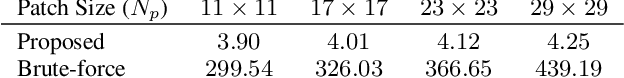
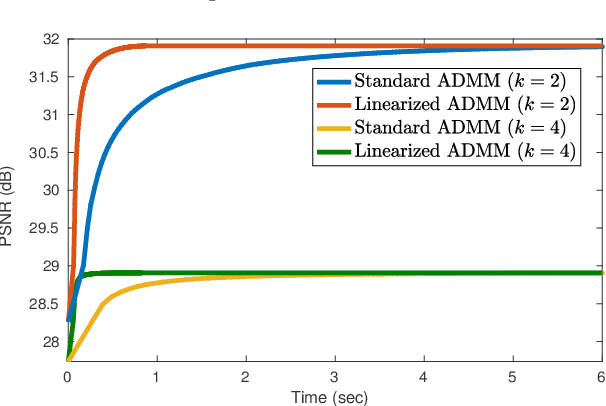
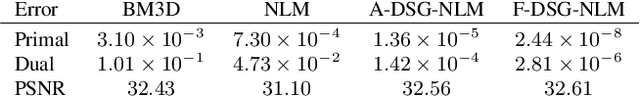
In plug-and-play image restoration, the regularization is performed using powerful denoisers such as nonlocal means (NLM) or BM3D. This is done within the framework of alternating direction method of multipliers (ADMM), where the regularization step is formally replaced by an off-the-shelf denoiser. Each plug-and-play iteration involves the inversion of the forward model followed by a denoising step. In this paper, we present a couple of ideas for improving the efficiency of the inversion and denoising steps. First, we propose to use linearized ADMM, which generally allows us to perform the inversion at a lower cost than standard ADMM. Moreover, we can easily incorporate hard constraints into the optimization framework as a result. Second, we develop a fast algorithm for doubly stochastic NLM, originally proposed by Sreehari et al. (IEEE TCI, 2016), which is about 80x faster than brute-force computation. This particular denoiser can be expressed as the proximal map of a convex regularizer and, as a consequence, we can guarantee convergence for linearized plug-and-play ADMM. We demonstrate the effectiveness of our proposals for super-resolution and single-photon imaging.

Artifact reduction for separable non-local means

It was recently demonstrated [J. Electron. Imaging, 25(2), 2016] that one can perform fast non-local means (NLM) denoising of one-dimensional signals using a method called lifting. The cost of lifting is independent of the patch length, which dramatically reduces the run-time for large patches. Unfortunately, it is difficult to directly extend lifting for non-local means denoising of images. To bypass this, the authors proposed a separable approximation in which the image rows and columns are filtered using lifting. The overall algorithm is significantly faster than NLM, and the results are comparable in terms of PSNR. However, the separable processing often produces vertical and horizontal stripes in the image. This problem was previously addressed by using a bilateral filter-based post-smoothing, which was effective in removing some of the stripes. In this letter, we demonstrate that stripes can be mitigated in the first place simply by involving the neighboring rows (or columns) in the filtering. In other words, we use a two-dimensional search (similar to NLM), while still using one-dimensional patches (as in the previous proposal). The novelty is in the observation that one can use lifting for performing two-dimensional searches. The proposed approach produces artifact-free images, whose quality and PSNR are comparable to NLM, while being significantly faster.

Pruned non-local means

In Non-Local Means (NLM), each pixel is denoised by performing a weighted averaging of its neighboring pixels, where the weights are computed using image patches. We demonstrate that the denoising performance of NLM can be improved by pruning the neighboring pixels, namely, by rejecting neighboring pixels whose weights are below a certain threshold $\lambda$. While pruning can potentially reduce pixel averaging in uniform-intensity regions, we demonstrate that there is generally an overall improvement in the denoising performance. In particular, the improvement comes from pixels situated close to edges and corners. The success of the proposed method strongly depends on the choice of the global threshold $\lambda$, which in turn depends on the noise level and the image characteristics. We show how Stein's unbiased estimator of the mean-squared error can be used to optimally tune $\lambda$, at a marginal computational overhead. We present some representative denoising results to demonstrate the superior performance of the proposed method over NLM and its variants.

Fast and High-Quality Bilateral Filtering Using Gauss-Chebyshev Approximation

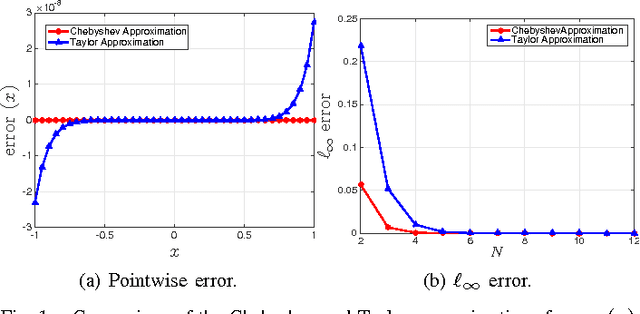
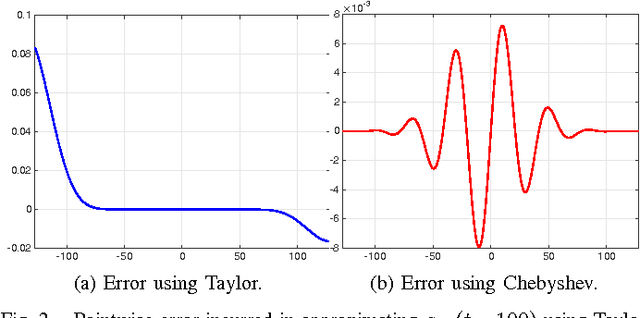
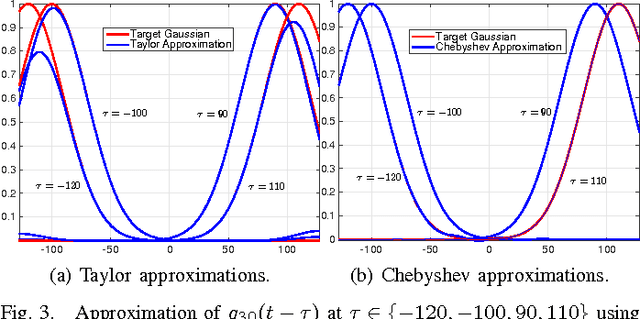
The bilateral filter is an edge-preserving smoother that has diverse applications in image processing, computer vision, computer graphics, and computational photography. The filter uses a spatial kernel along with a range kernel to perform edge-preserving smoothing. In this paper, we consider the Gaussian bilateral filter where both the kernels are Gaussian. A direct implementation of the Gaussian bilateral filter requires $O(\sigma_s^2)$ operations per pixel, where $\sigma_s$ is the standard deviation of the spatial Gaussian. In fact, it is well-known that the direct implementation is slow in practice. We present an approximation of the Gaussian bilateral filter, whereby we can cut down the number of operations to $O(1)$ per pixel for any arbitrary $\sigma_s$, and yet achieve very high-quality filtering that is almost indistinguishable from the output of the original filter. We demonstrate that the proposed approximation is few orders faster in practice compared to the direct implementation. We also demonstrate that the approximation is competitive with existing fast algorithms in terms of speed and accuracy.

Fast Bilateral Filtering of Vector-Valued Images

In this paper, we consider a natural extension of the edge-preserving bilateral filter for vector-valued images. The direct computation of this non-linear filter is slow in practice. We demonstrate how a fast algorithm can be obtained by first approximating the Gaussian kernel of the bilateral filter using raised-cosines, and then using Monte Carlo sampling. We present simulation results on color images to demonstrate the accuracy of the algorithm and the speedup over the direct implementation.

On Fast Bilateral Filtering using Fourier Kernels

It was demonstrated in earlier work that, by approximating its range kernel using shiftable functions, the non-linear bilateral filter can be computed using a series of fast convolutions. Previous approaches based on shiftable approximation have, however, been restricted to Gaussian range kernels. In this work, we propose a novel approximation that can be applied to any range kernel, provided it has a pointwise-convergent Fourier series. More specifically, we propose to approximate the Gaussian range kernel of the bilateral filter using a Fourier basis, where the coefficients of the basis are obtained by solving a series of least-squares problems. The coefficients can be efficiently computed using a recursive form of the QR decomposition. By controlling the cardinality of the Fourier basis, we can obtain a good tradeoff between the run-time and the filtering accuracy. In particular, we are able to guarantee sub-pixel accuracy for the overall filtering, which is not provided by most existing methods for fast bilateral filtering. We present simulation results to demonstrate the speed and accuracy of the proposed algorithm.