Scan-specific Self-supervised Bayesian Deep Non-linear Inversion for Undersampled MRI Reconstruction

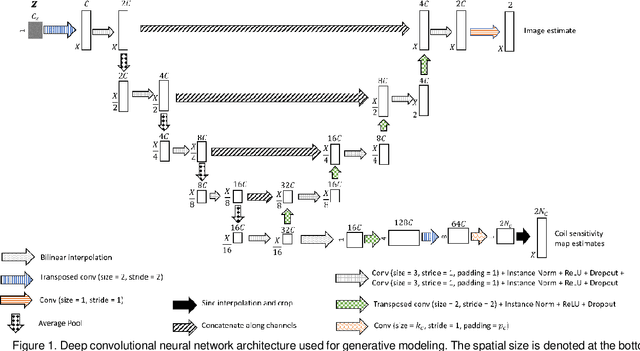
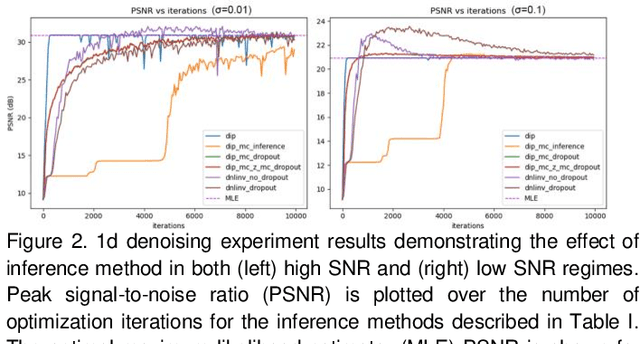
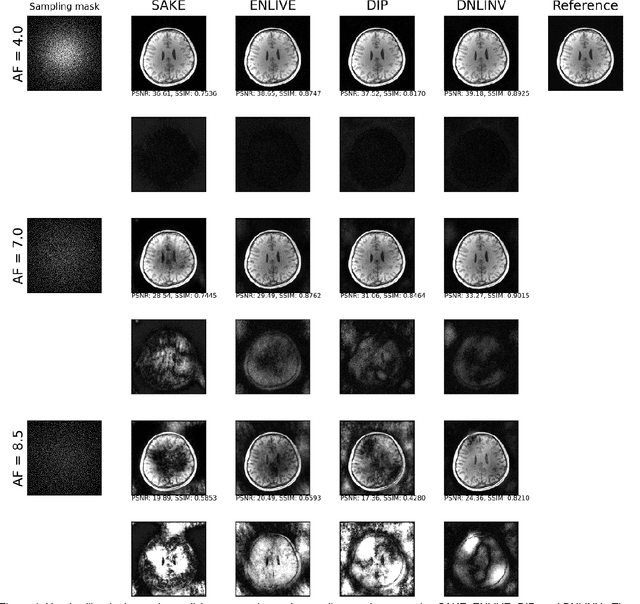
Magnetic resonance imaging is subject to slow acquisition times due to the inherent limitations in data sampling. Recently, supervised deep learning has emerged as a promising technique for reconstructing sub-sampled MRI. However, supervised deep learning requires a large dataset of fully-sampled data. Although unsupervised or self-supervised deep learning methods have emerged to address the limitations of supervised deep learning approaches, they still require a database of images. In contrast, scan-specific deep learning methods learn and reconstruct using only the sub-sampled data from a single scan. Current scan-specific approaches require a fully-sampled auto calibration scan region in k-space that cost additional scan time. Here, we introduce Scan-Specific Self-Supervised Bayesian Deep Non-Linear Inversion (DNLINV) that does not require an auto calibration scan region. DNLINV utilizes a deep image prior-type generative modeling approach and relies on approximate Bayesian inference to regularize the deep convolutional neural network. We demonstrate our approach on several anatomies, contrasts, and sampling patterns and show improved performance over existing approaches in scan-specific calibrationless parallel imaging and compressed sensing.

Efficient Hierarchical Bayesian Inference for Spatio-temporal Regression Models in Neuroimaging

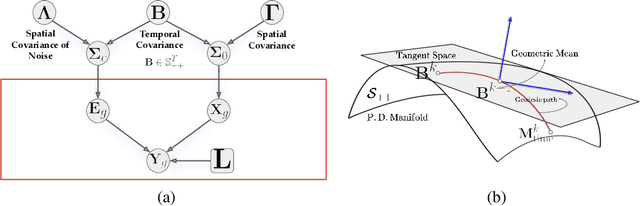
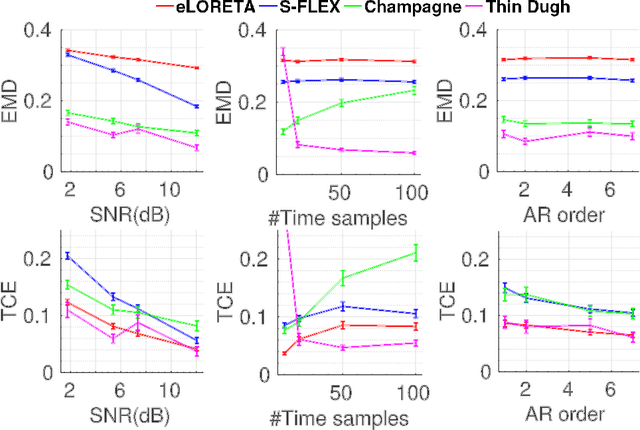
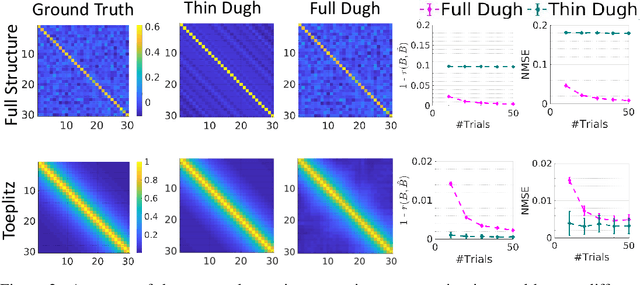
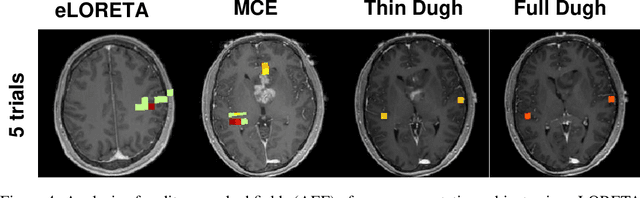
Several problems in neuroimaging and beyond require inference on the parameters of multi-task sparse hierarchical regression models. Examples include M/EEG inverse problems, neural encoding models for task-based fMRI analyses, and climate science. In these domains, both the model parameters to be inferred and the measurement noise may exhibit a complex spatio-temporal structure. Existing work either neglects the temporal structure or leads to computationally demanding inference schemes. Overcoming these limitations, we devise a novel flexible hierarchical Bayesian framework within which the spatio-temporal dynamics of model parameters and noise are modeled to have Kronecker product covariance structure. Inference in our framework is based on majorization-minimization optimization and has guaranteed convergence properties. Our highly efficient algorithms exploit the intrinsic Riemannian geometry of temporal autocovariance matrices. For stationary dynamics described by Toeplitz matrices, the theory of circulant embeddings is employed. We prove convex bounding properties and derive update rules of the resulting algorithms. On both synthetic and real neural data from M/EEG, we demonstrate that our methods lead to improved performance.