Enhancing Brain Source Reconstruction through Physics-Informed 3D Neural Networks

Reconstructing brain sources is a fundamental challenge in neuroscience, crucial for understanding brain function and dysfunction. Electroencephalography (EEG) signals have a high temporal resolution. However, identifying the correct spatial location of brain sources from these signals remains difficult due to the ill-posed structure of the problem. Traditional methods predominantly rely on manually crafted priors, missing the flexibility of data-driven learning, while recent deep learning approaches focus on end-to-end learning, typically using the physical information of the forward model only for generating training data. We propose the novel hybrid method 3D-PIUNet for EEG source localization that effectively integrates the strengths of traditional and deep learning techniques. 3D-PIUNet starts from an initial physics-informed estimate by using the pseudo inverse to map from measurements to source space. Secondly, by viewing the brain as a 3D volume, we use a 3D convolutional U-Net to capture spatial dependencies and refine the solution according to the learned data prior. Training the model relies on simulated pseudo-realistic brain source data, covering different source distributions. Trained on this data, our model significantly improves spatial accuracy, demonstrating superior performance over both traditional and end-to-end data-driven methods. Additionally, we validate our findings with real EEG data from a visual task, where 3D-PIUNet successfully identifies the visual cortex and reconstructs the expected temporal behavior, thereby showcasing its practical applicability.

Efficient Hierarchical Bayesian Inference for Spatio-temporal Regression Models in Neuroimaging

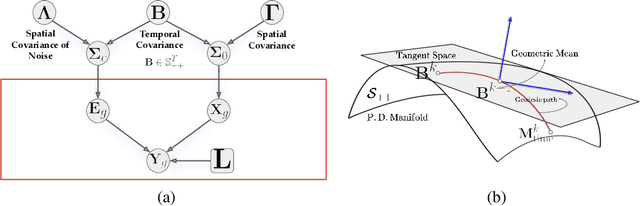
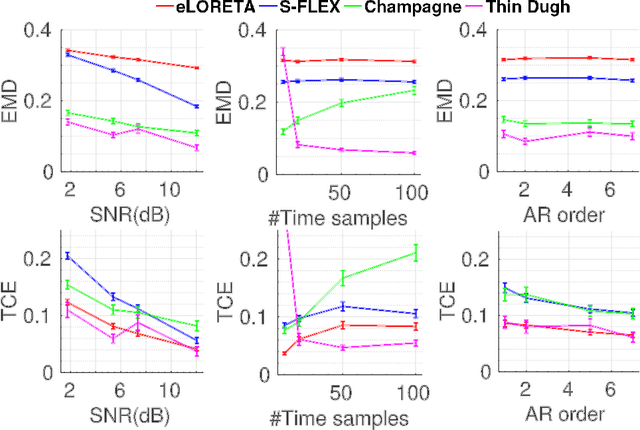
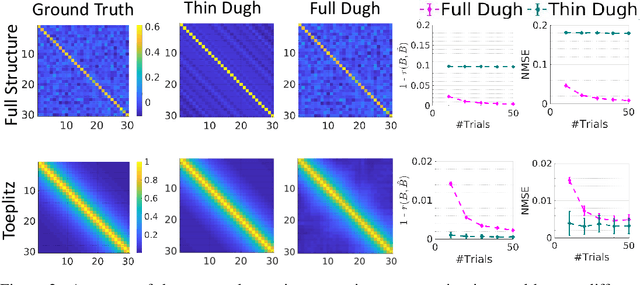
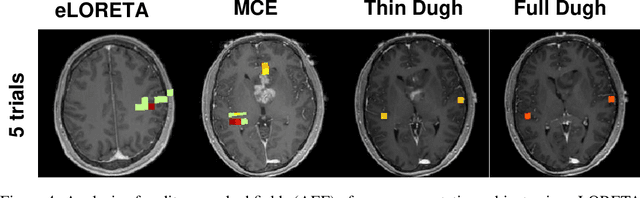
Several problems in neuroimaging and beyond require inference on the parameters of multi-task sparse hierarchical regression models. Examples include M/EEG inverse problems, neural encoding models for task-based fMRI analyses, and climate science. In these domains, both the model parameters to be inferred and the measurement noise may exhibit a complex spatio-temporal structure. Existing work either neglects the temporal structure or leads to computationally demanding inference schemes. Overcoming these limitations, we devise a novel flexible hierarchical Bayesian framework within which the spatio-temporal dynamics of model parameters and noise are modeled to have Kronecker product covariance structure. Inference in our framework is based on majorization-minimization optimization and has guaranteed convergence properties. Our highly efficient algorithms exploit the intrinsic Riemannian geometry of temporal autocovariance matrices. For stationary dynamics described by Toeplitz matrices, the theory of circulant embeddings is employed. We prove convex bounding properties and derive update rules of the resulting algorithms. On both synthetic and real neural data from M/EEG, we demonstrate that our methods lead to improved performance.