Fast and High-Quality Bilateral Filtering Using Gauss-Chebyshev Approximation
Paper and Code
May 10, 2016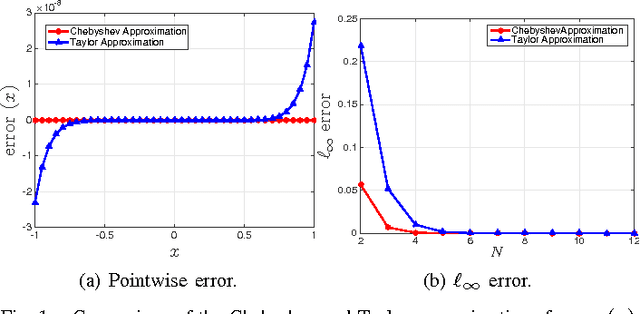
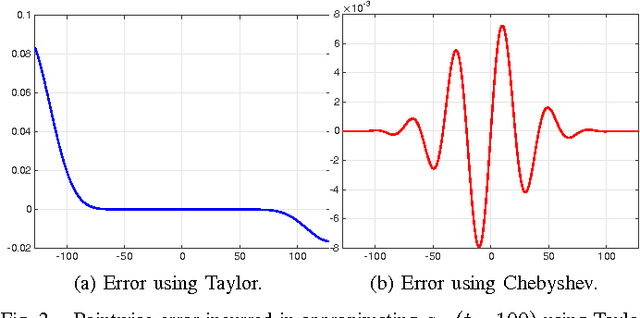
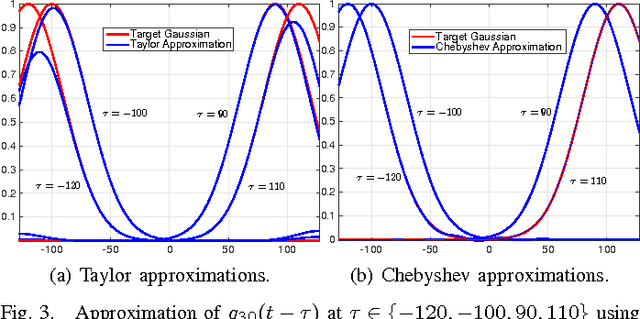

The bilateral filter is an edge-preserving smoother that has diverse applications in image processing, computer vision, computer graphics, and computational photography. The filter uses a spatial kernel along with a range kernel to perform edge-preserving smoothing. In this paper, we consider the Gaussian bilateral filter where both the kernels are Gaussian. A direct implementation of the Gaussian bilateral filter requires $O(\sigma_s^2)$ operations per pixel, where $\sigma_s$ is the standard deviation of the spatial Gaussian. In fact, it is well-known that the direct implementation is slow in practice. We present an approximation of the Gaussian bilateral filter, whereby we can cut down the number of operations to $O(1)$ per pixel for any arbitrary $\sigma_s$, and yet achieve very high-quality filtering that is almost indistinguishable from the output of the original filter. We demonstrate that the proposed approximation is few orders faster in practice compared to the direct implementation. We also demonstrate that the approximation is competitive with existing fast algorithms in terms of speed and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge