Sam Greydanus
The Cursive Transformer
Mar 31, 2025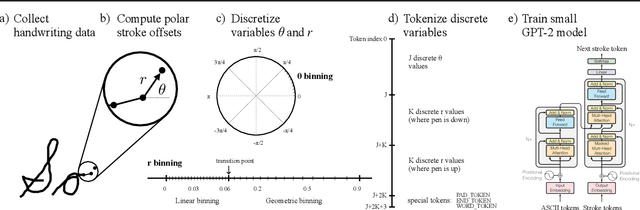
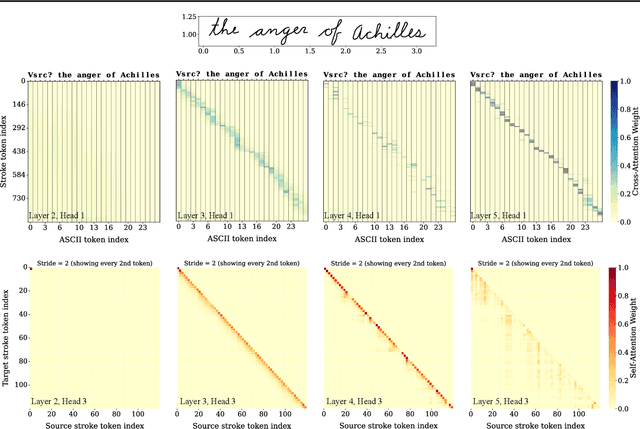

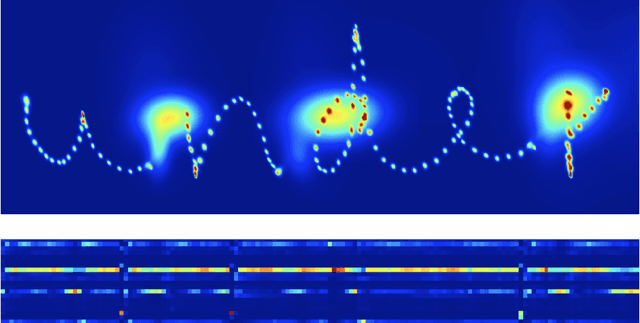
Abstract:Transformers trained on tokenized text, audio, and images can generate high-quality autoregressive samples. But handwriting data, represented as sequences of pen coordinates, remains underexplored. We introduce a novel tokenization scheme that converts pen stroke offsets to polar coordinates, discretizes them into bins, and then turns them into sequences of tokens with which to train a standard GPT model. This allows us to capture complex stroke distributions without using any specialized architectures (eg. the mixture density network or the self-advancing ASCII attention head from Graves 2014). With just 3,500 handwritten words and a few simple data augmentations, we are able to train a model that can generate realistic cursive handwriting. Our approach is simpler and more performant than previous RNN-based methods.
Nature's Cost Function: Simulating Physics by Minimizing the Action
Mar 03, 2023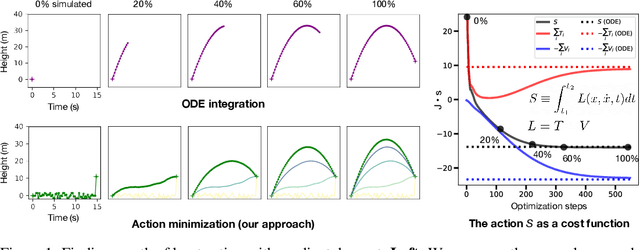

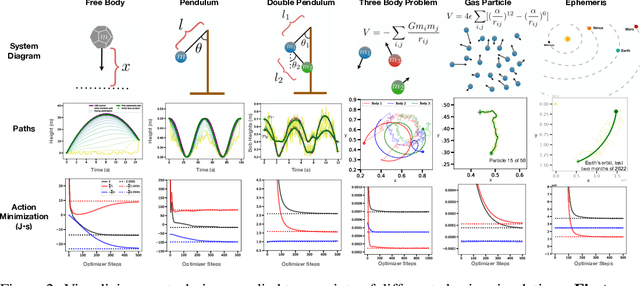
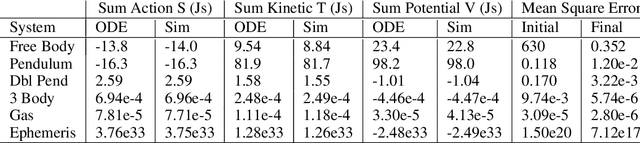
Abstract:In physics, there is a scalar function called the action which behaves like a cost function. When minimized, it yields the "path of least action" which represents the path a physical system will take through space and time. This function is crucial in theoretical physics and is usually minimized analytically to obtain equations of motion for various problems. In this paper, we propose a different approach: instead of minimizing the action analytically, we discretize it and then minimize it directly with gradient descent. We use this approach to obtain dynamics for six different physical systems and show that they are nearly identical to ground-truth dynamics. We discuss failure modes such as the unconstrained energy effect and show how to address them. Finally, we use the discretized action to construct a simple but novel quantum simulation.
Dissipative Hamiltonian Neural Networks: Learning Dissipative and Conservative Dynamics Separately
Jan 26, 2022



Abstract:Understanding natural symmetries is key to making sense of our complex and ever-changing world. Recent work has shown that neural networks can learn such symmetries directly from data using Hamiltonian Neural Networks (HNNs). But HNNs struggle when trained on datasets where energy is not conserved. In this paper, we ask whether it is possible to identify and decompose conservative and dissipative dynamics simultaneously. We propose Dissipative Hamiltonian Neural Networks (D-HNNs), which parameterize both a Hamiltonian and a Rayleigh dissipation function. Taken together, they represent an implicit Helmholtz decomposition which can separate dissipative effects such as friction from symmetries such as conservation of energy. We train our model to decompose a damped mass-spring system into its friction and inertial terms and then show that this decomposition can be used to predict dynamics for unseen friction coefficients. Then we apply our model to real world data including a large, noisy ocean current dataset where decomposing the velocity field yields useful scientific insights.
Piecewise-constant Neural ODEs
Jun 11, 2021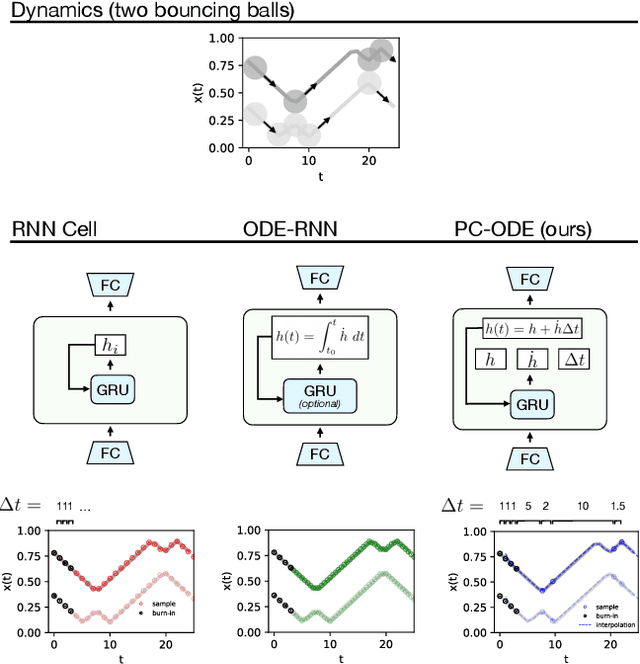
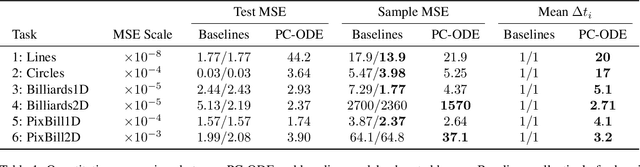
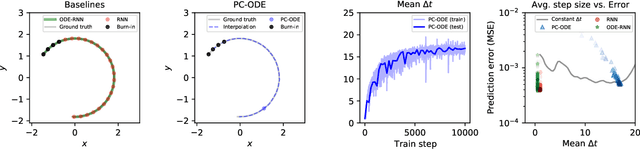

Abstract:Neural networks are a popular tool for modeling sequential data but they generally do not treat time as a continuous variable. Neural ODEs represent an important exception: they parameterize the time derivative of a hidden state with a neural network and then integrate over arbitrary amounts of time. But these parameterizations, which have arbitrary curvature, can be hard to integrate and thus train and evaluate. In this paper, we propose making a piecewise-constant approximation to Neural ODEs to mitigate these issues. Our model can be integrated exactly via Euler integration and can generate autoregressive samples in 3-20 times fewer steps than comparable RNN and ODE-RNN models. We evaluate our model on several synthetic physics tasks and a planning task inspired by the game of billiards. We find that it matches the performance of baseline approaches while requiring less time to train and evaluate.
Scaling down Deep Learning
Dec 04, 2020



Abstract:Though deep learning models have taken on commercial and political relevance, many aspects of their training and operation remain poorly understood. This has sparked interest in "science of deep learning" projects, many of which are run at scale and require enormous amounts of time, money, and electricity. But how much of this research really needs to occur at scale? In this paper, we introduce MNIST-1D: a minimalist, low-memory, and low-compute alternative to classic deep learning benchmarks. The training examples are 20 times smaller than MNIST examples yet they differentiate more clearly between linear, nonlinear, and convolutional models which attain 32, 68, and 94% accuracy respectively (these models obtain 94, 99+, and 99+% on MNIST). Then we present example use cases which include measuring the spatial inductive biases of lottery tickets, observing deep double descent, and metalearning an activation function.
Lagrangian Neural Networks
Mar 10, 2020



Abstract:Accurate models of the world are built upon notions of its underlying symmetries. In physics, these symmetries correspond to conservation laws, such as for energy and momentum. Yet even though neural network models see increasing use in the physical sciences, they struggle to learn these symmetries. In this paper, we propose Lagrangian Neural Networks (LNNs), which can parameterize arbitrary Lagrangians using neural networks. In contrast to models that learn Hamiltonians, LNNs do not require canonical coordinates, and thus perform well in situations where canonical momenta are unknown or difficult to compute. Unlike previous approaches, our method does not restrict the functional form of learned energies and will produce energy-conserving models for a variety of tasks. We test our approach on a double pendulum and a relativistic particle, demonstrating energy conservation where a baseline approach incurs dissipation and modeling relativity without canonical coordinates where a Hamiltonian approach fails. Finally, we show how this model can be applied to graphs and continuous systems using a Lagrangian Graph Network, and demonstrate it on the 1D wave equation.
Neural reparameterization improves structural optimization
Sep 14, 2019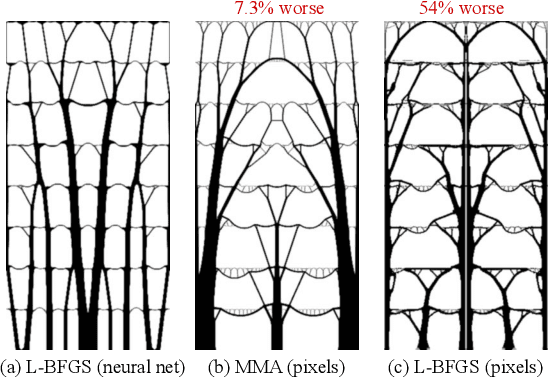
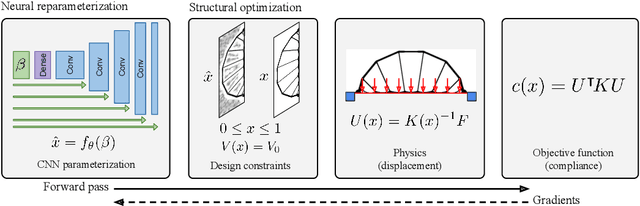
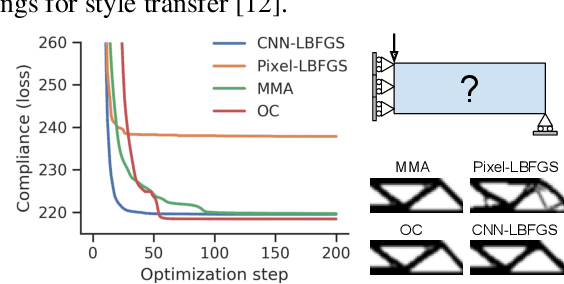
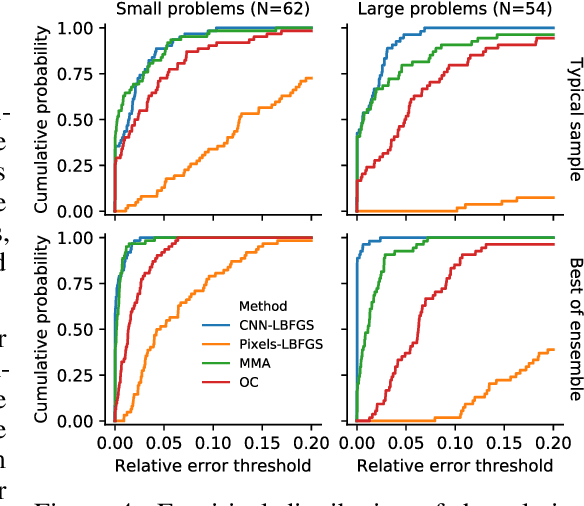
Abstract:Structural optimization is a popular method for designing objects such as bridge trusses, airplane wings, and optical devices. Unfortunately, the quality of solutions depends heavily on how the problem is parameterized. In this paper, we propose using the implicit bias over functions induced by neural networks to improve the parameterization of structural optimization. Rather than directly optimizing densities on a grid, we instead optimize the parameters of a neural network which outputs those densities. This reparameterization leads to different and often better solutions. On a selection of 116 structural optimization tasks, our approach produces the best design 50% more often than the best baseline method.
Hamiltonian Neural Networks
Jul 07, 2019



Abstract:Even though neural networks enjoy widespread use, they still struggle to learn the basic laws of physics. How might we endow them with better inductive biases? In this paper, we draw inspiration from Hamiltonian mechanics to train models that learn and respect exact conservation laws in an unsupervised manner. We evaluate our models on problems where conservation of energy is important, including the two-body problem and pixel observations of a pendulum. Our model trains faster and generalizes better than a regular neural network. An interesting side effect is that our model is perfectly reversible in time.
Learning Finite State Representations of Recurrent Policy Networks
Nov 29, 2018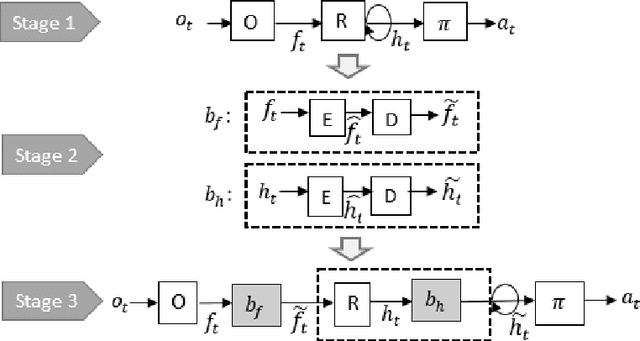



Abstract:Recurrent neural networks (RNNs) are an effective representation of control policies for a wide range of reinforcement and imitation learning problems. RNN policies, however, are particularly difficult to explain, understand, and analyze due to their use of continuous-valued memory vectors and observation features. In this paper, we introduce a new technique, Quantized Bottleneck Insertion, to learn finite representations of these vectors and features. The result is a quantized representation of the RNN that can be analyzed to improve our understanding of memory use and general behavior. We present results of this approach on synthetic environments and six Atari games. The resulting finite representations are surprisingly small in some cases, using as few as 3 discrete memory states and 10 observations for a perfect Pong policy. We also show that these finite policy representations lead to improved interpretability.
Visualizing and Understanding Atari Agents
Sep 10, 2018
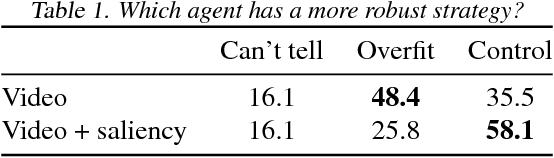
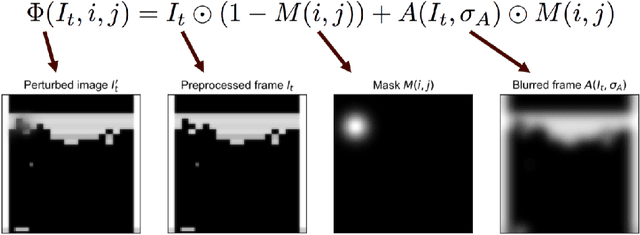

Abstract:While deep reinforcement learning (deep RL) agents are effective at maximizing rewards, it is often unclear what strategies they use to do so. In this paper, we take a step toward explaining deep RL agents through a case study using Atari 2600 environments. In particular, we focus on using saliency maps to understand how an agent learns and executes a policy. We introduce a method for generating useful saliency maps and use it to show 1) what strong agents attend to, 2) whether agents are making decisions for the right or wrong reasons, and 3) how agents evolve during learning. We also test our method on non-expert human subjects and find that it improves their ability to reason about these agents. Overall, our results show that saliency information can provide significant insight into an RL agent's decisions and learning behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge