ALLaM: Large Language Models for Arabic and English

We present ALLaM: Arabic Large Language Model, a series of large language models to support the ecosystem of Arabic Language Technologies (ALT). ALLaM is carefully trained considering the values of language alignment and knowledge transfer at scale. Our autoregressive decoder-only architecture models demonstrate how second-language acquisition via vocabulary expansion and pretraining on a mixture of Arabic and English text can steer a model towards a new language (Arabic) without any catastrophic forgetting in the original language (English). Furthermore, we highlight the effectiveness of using parallel/translated data to aid the process of knowledge alignment between languages. Finally, we show that extensive alignment with human preferences can significantly enhance the performance of a language model compared to models of a larger scale with lower quality alignment. ALLaM achieves state-of-the-art performance in various Arabic benchmarks, including MMLU Arabic, ACVA, and Arabic Exams. Our aligned models improve both in Arabic and English from their base aligned models.

On Robust Learning from Noisy Labels: A Permutation Layer Approach

The existence of label noise imposes significant challenges (e.g., poor generalization) on the training process of deep neural networks (DNN). As a remedy, this paper introduces a permutation layer learning approach termed PermLL to dynamically calibrate the training process of the DNN subject to instance-dependent and instance-independent label noise. The proposed method augments the architecture of a conventional DNN by an instance-dependent permutation layer. This layer is essentially a convex combination of permutation matrices that is dynamically calibrated for each sample. The primary objective of the permutation layer is to correct the loss of noisy samples mitigating the effect of label noise. We provide two variants of PermLL in this paper: one applies the permutation layer to the model's prediction, while the other applies it directly to the given noisy label. In addition, we provide a theoretical comparison between the two variants and show that previous methods can be seen as one of the variants. Finally, we validate PermLL experimentally and show that it achieves state-of-the-art performance on both real and synthetic datasets.

Network Moments: Extensions and Sparse-Smooth Attacks

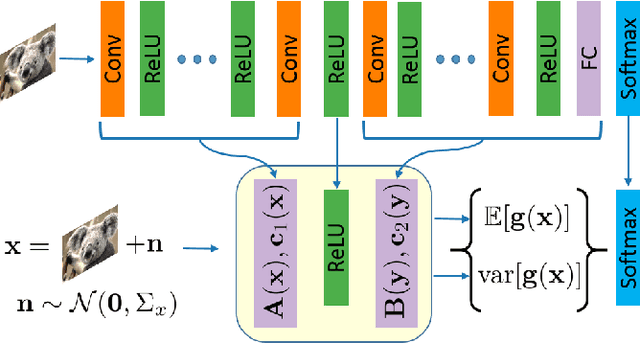
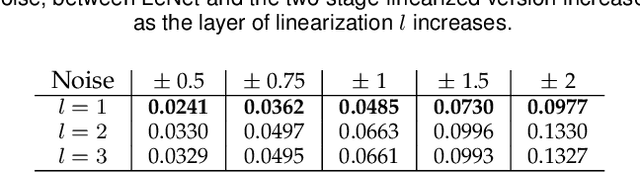
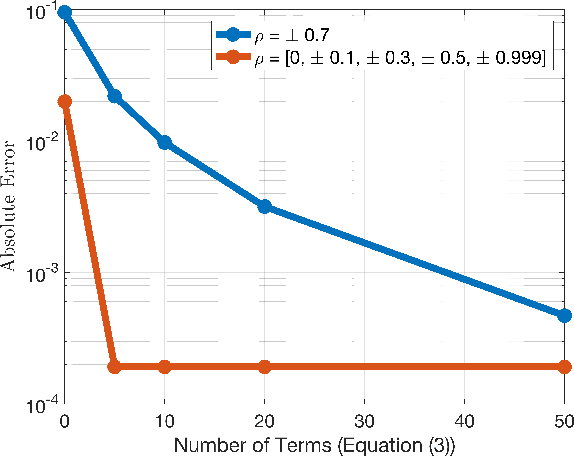
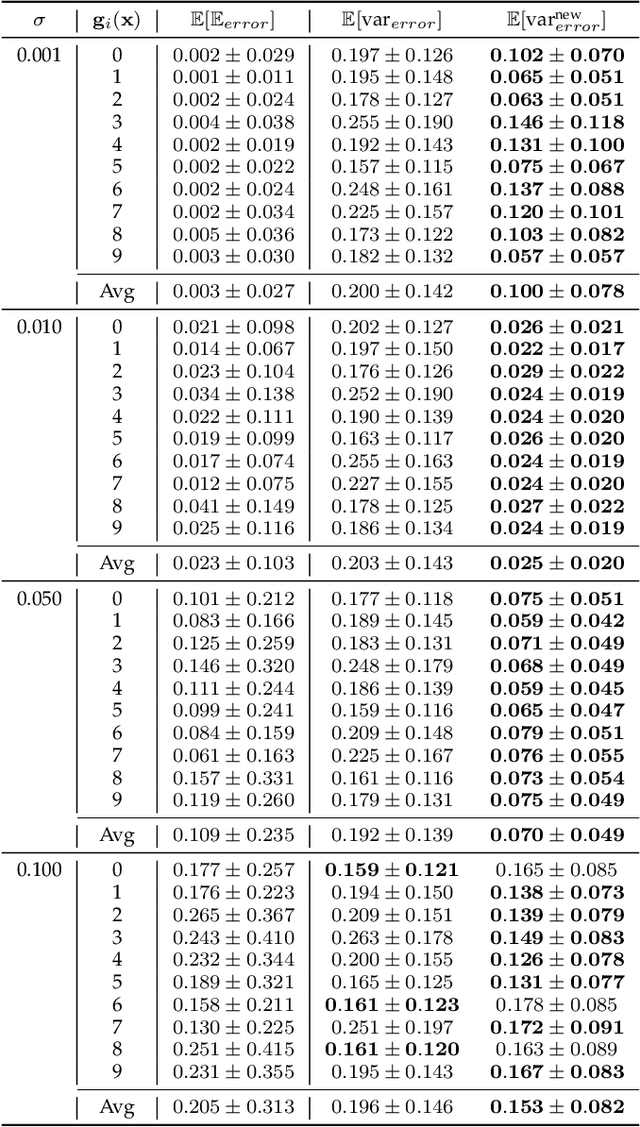
The impressive performance of deep neural networks (DNNs) has immensely strengthened the line of research that aims at theoretically analyzing their effectiveness. This has incited research on the reaction of DNNs to noisy input, namely developing adversarial input attacks and strategies that lead to robust DNNs to these attacks. To that end, in this paper, we derive exact analytic expressions for the first and second moments (mean and variance) of a small piecewise linear (PL) network (Affine, ReLU, Affine) subject to Gaussian input. In particular, we generalize the second-moment expression of Bibi et al. to arbitrary input Gaussian distributions, dropping the zero-mean assumption. We show that the new variance expression can be efficiently approximated leading to much tighter variance estimates as compared to the preliminary results of Bibi et al. Moreover, we experimentally show that these expressions are tight under simple linearizations of deeper PL-DNNs, where we investigate the effect of the linearization sensitivity on the accuracy of the moment estimates. Lastly, we show that the derived expressions can be used to construct sparse and smooth Gaussian adversarial attacks (targeted and non-targeted) that tend to lead to perceptually feasible input attacks.

Probabilistically True and Tight Bounds for Robust Deep Neural Network Training

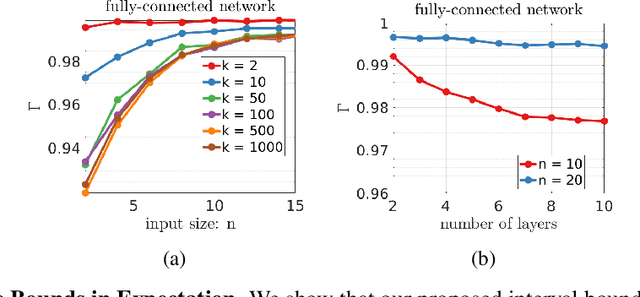
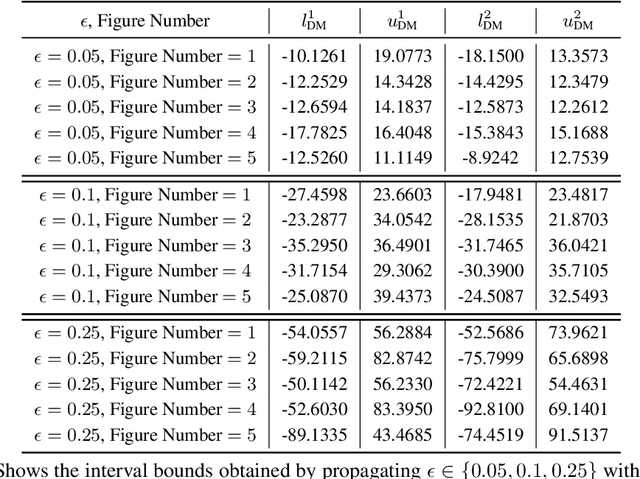
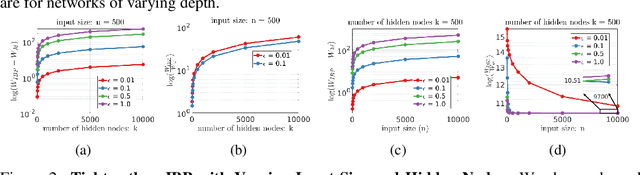
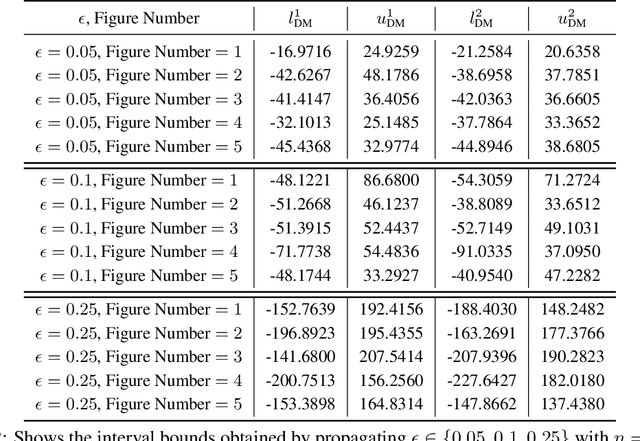
Training Deep Neural Networks (DNNs) that are robust to norm bounded adversarial attacks remains an elusive problem. While verification based methods are generally too expensive to robustly train large networks, it was demonstrated in Gowal et al. that bounded input intervals can be inexpensively propagated per layer through large networks. This interval bound propagation (IBP) approach lead to high robustness and was the first to be employed on large networks. However, due to the very loose nature of the IBP bounds, particularly for large networks, the required training procedure is complex and involved. In this paper, we closely examine the bounds of a block of layers composed of an affine layer followed by a ReLU nonlinearity followed by another affine layer. In doing so, we propose probabilistic bounds, true bounds with overwhelming probability, that are provably tighter than IBP bounds in expectation. We then extend this result to deeper networks through blockwise propagation and show that we can achieve orders of magnitudes tighter bounds compared to IBP. With such tight bounds, we demonstrate that a simple standard training procedure can achieve the best robustness-accuracy trade-off across several architectures on both MNIST and CIFAR10.