On Robust Learning from Noisy Labels: A Permutation Layer Approach

The existence of label noise imposes significant challenges (e.g., poor generalization) on the training process of deep neural networks (DNN). As a remedy, this paper introduces a permutation layer learning approach termed PermLL to dynamically calibrate the training process of the DNN subject to instance-dependent and instance-independent label noise. The proposed method augments the architecture of a conventional DNN by an instance-dependent permutation layer. This layer is essentially a convex combination of permutation matrices that is dynamically calibrated for each sample. The primary objective of the permutation layer is to correct the loss of noisy samples mitigating the effect of label noise. We provide two variants of PermLL in this paper: one applies the permutation layer to the model's prediction, while the other applies it directly to the given noisy label. In addition, we provide a theoretical comparison between the two variants and show that previous methods can be seen as one of the variants. Finally, we validate PermLL experimentally and show that it achieves state-of-the-art performance on both real and synthetic datasets.

Proximal Splitting Networks for Image Restoration

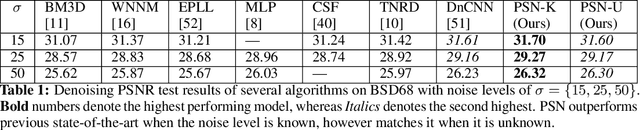
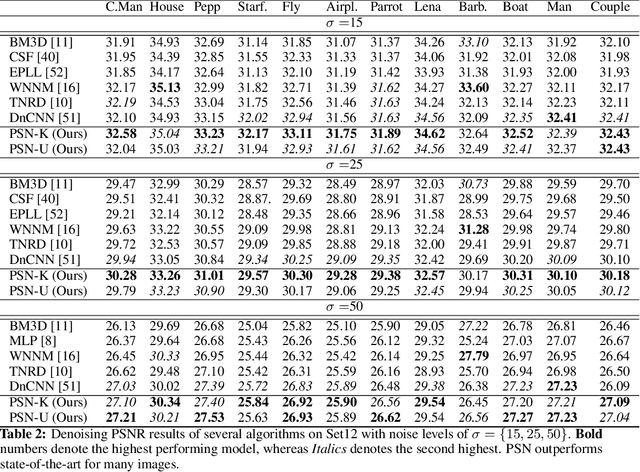
Image restoration problems are typically ill-posed requiring the design of suitable priors. These priors are typically hand-designed and are fully instantiated throughout the process. In this paper, we introduce a novel framework for handling inverse problems related to image restoration based on elements from the half quadratic splitting method and proximal operators. Modeling the proximal operator as a convolutional network, we defined an implicit prior on the image space as a function class during training. This is in contrast to the common practice in literature of having the prior to be fixed and fully instantiated even during training stages. Further, we allow this proximal operator to be tuned differently for each iteration which greatly increases modeling capacity and allows us to reduce the number of iterations by an order of magnitude as compared to other approaches. Our final network is an end-to-end one whose run time matches the previous fastest algorithms while outperforming them in recovery fidelity on two image restoration tasks. Indeed, we find our approach achieves state-of-the-art results on benchmarks in image denoising and image super resolution while recovering more complex and finer details.