Towards a Hypothesis on Visual Transformation based Self-Supervision

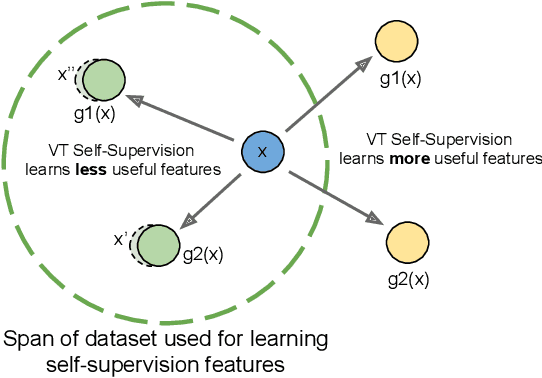
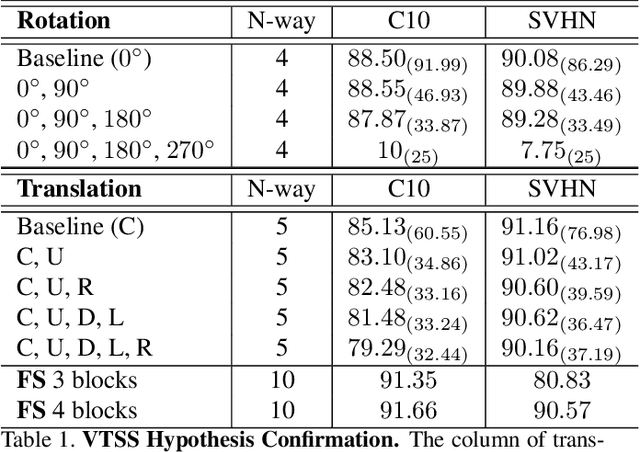
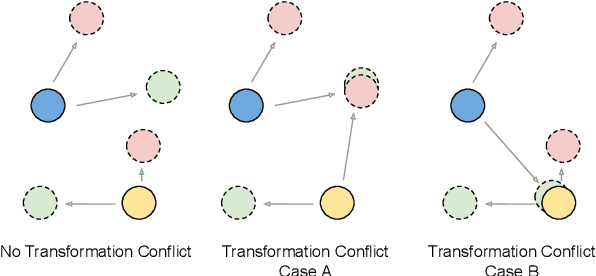
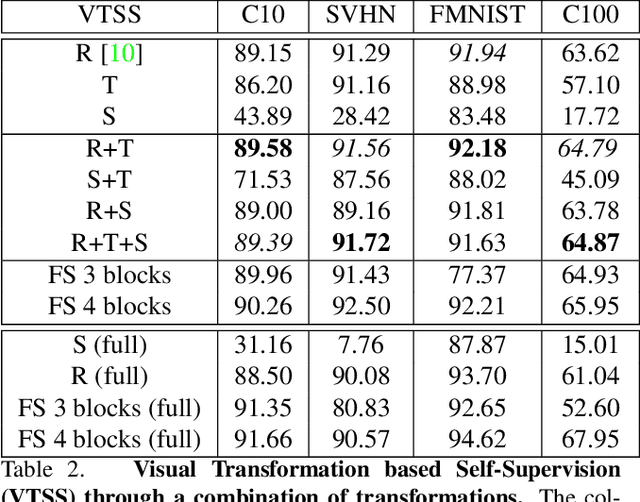
We propose the first qualitative hypothesis characterizing the behavior of visual transformation based self-supervision, called the VTSS hypothesis. Given a dataset upon which a self-supervised task is performed while predicting instantiations of a transformation, the hypothesis states that if the predicted instantiations of the transformations are already present in the dataset, then the representation learned will be less useful. The hypothesis was derived by observing a key constraint in the application of self-supervision using a particular transformation. This constraint, which we term the transformation conflict for this paper, forces a network learn degenerative features thereby reducing the usefulness of the representation. The VTSS hypothesis helps us identify transformations that have the potential to be effective as a self-supervision task. Further, it helps to generally predict whether a particular transformation based self-supervision technique would be effective or not for a particular dataset. We provide extensive evaluations on CIFAR 10, CIFAR 100, SVHN and FMNIST confirming the hypothesis and the trends it predicts. We also propose novel cost-effective self-supervision techniques based on translation and scale, which when combined with rotation outperforms all transformations applied individually. Overall, this paper aims to shed light on the phenomenon of visual transformation based self-supervision.

Learning Non-Parametric Invariances from Data with Permanent Random Connectomes

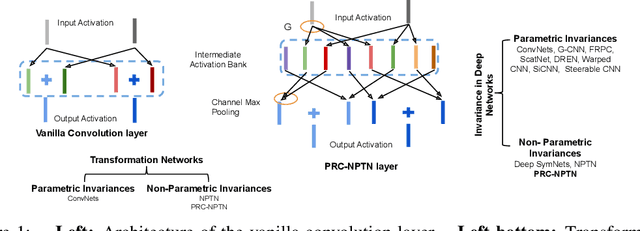
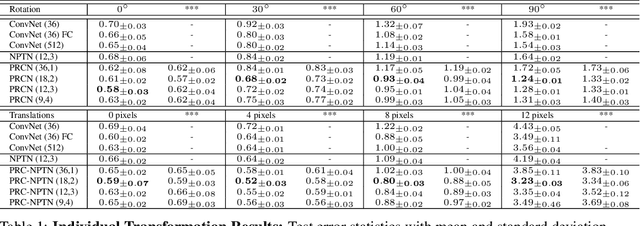
One of the fundamental problems in supervised classification and in machine learning in general, is the modelling of non-parametric invariances that exist in data. Most prior art has focused on enforcing priors in the form of invariances to parametric nuisance transformations that are expected to be present in data. Learning non-parametric invariances directly from data remains an important open problem. In this paper, we introduce a new architectural layer for convolutional networks which is capable of learning general invariances from data itself. This layer can learn invariance to non-parametric transformations and interestingly, motivates and incorporates permanent random connectomes, thereby being called Permanent Random Connectome Non-Parametric Transformation Networks (PRC-NPTN). PRC-NPTN networks are initialized with random connections (not just weights) which are a small subset of the connections in a fully connected convolution layer. Importantly, these connections in PRC-NPTNs once initialized remain permanent throughout training and testing. Permanent random connectomes make these architectures loosely more biologically plausible than many other mainstream network architectures which require highly ordered structures. We motivate randomly initialized connections as a simple method to learn invariance from data itself while invoking invariance towards multiple nuisance transformations simultaneously. We find that these randomly initialized permanent connections have positive effects on generalization, outperform much larger ConvNet baselines and the recently proposed Non-Parametric Transformation Network (NPTN) on benchmarks that enforce learning invariances from the data itself.

Proximal Splitting Networks for Image Restoration

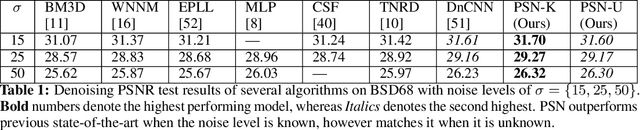
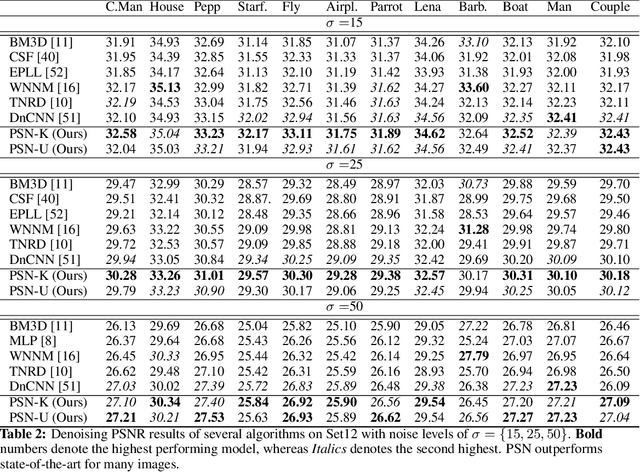
Image restoration problems are typically ill-posed requiring the design of suitable priors. These priors are typically hand-designed and are fully instantiated throughout the process. In this paper, we introduce a novel framework for handling inverse problems related to image restoration based on elements from the half quadratic splitting method and proximal operators. Modeling the proximal operator as a convolutional network, we defined an implicit prior on the image space as a function class during training. This is in contrast to the common practice in literature of having the prior to be fixed and fully instantiated even during training stages. Further, we allow this proximal operator to be tuned differently for each iteration which greatly increases modeling capacity and allows us to reduce the number of iterations by an order of magnitude as compared to other approaches. Our final network is an end-to-end one whose run time matches the previous fastest algorithms while outperforming them in recovery fidelity on two image restoration tasks. Indeed, we find our approach achieves state-of-the-art results on benchmarks in image denoising and image super resolution while recovering more complex and finer details.

Non-Parametric Transformation Networks

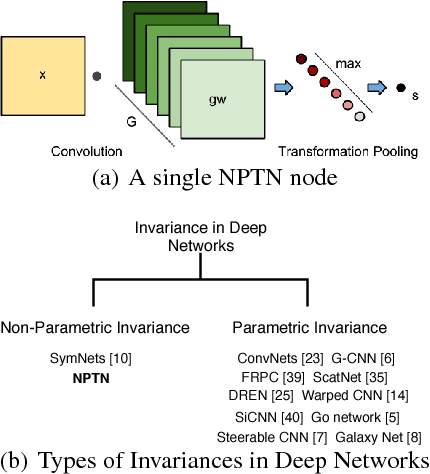
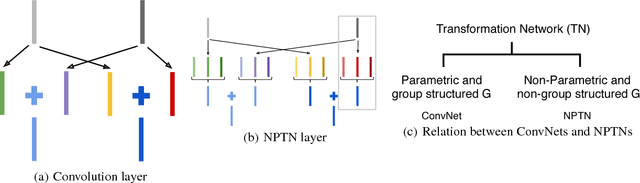
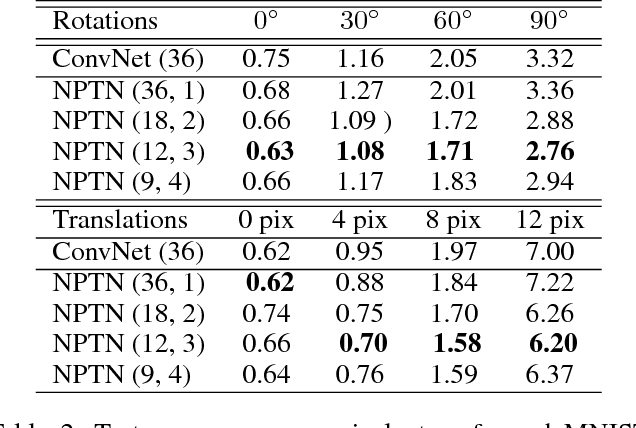
ConvNets, through their architecture, only enforce invariance to translation. In this paper, we introduce a new class of deep convolutional architectures called Non-Parametric Transformation Networks (NPTNs) which can learn \textit{general} invariances and symmetries directly from data. NPTNs are a natural generalization of ConvNets and can be optimized directly using gradient descent. Unlike almost all previous works in deep architectures, they make no assumption regarding the structure of the invariances present in the data and in that aspect are flexible and powerful. We also model ConvNets and NPTNs under a unified framework called Transformation Networks (TN), which yields a better understanding of the connection between the two. We demonstrate the efficacy of NPTNs on data such as MNIST with extreme transformations and CIFAR10 where they outperform baselines, and further outperform several recent algorithms on ETH-80. They do so while having the same number of parameters. We also show that they are more effective than ConvNets in modelling symmetries and invariances from data, without the explicit knowledge of the added arbitrary nuisance transformations. Finally, we replace ConvNets with NPTNs within Capsule Networks and show that this enables Capsule Nets to perform even better.

Ring loss: Convex Feature Normalization for Face Recognition

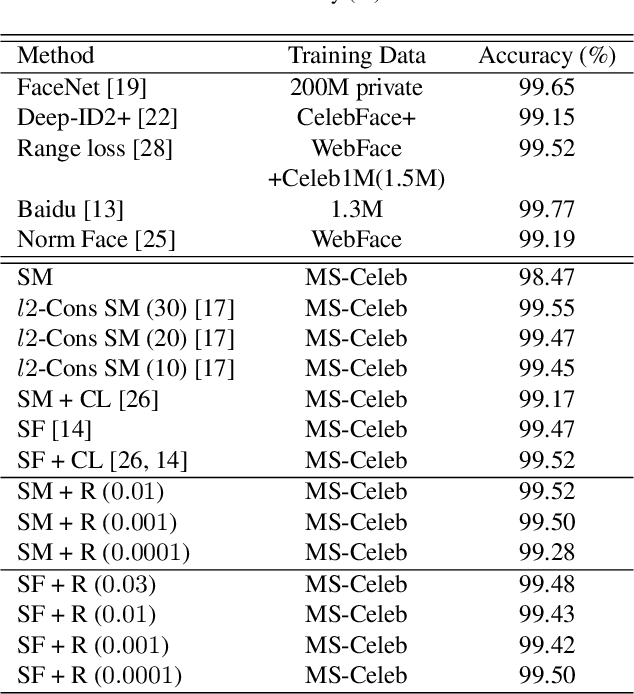
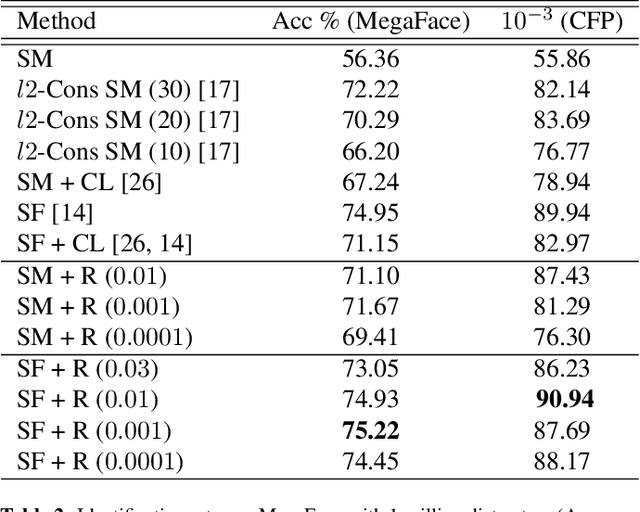
We motivate and present Ring loss, a simple and elegant feature normalization approach for deep networks designed to augment standard loss functions such as Softmax. We argue that deep feature normalization is an important aspect of supervised classification problems where we require the model to represent each class in a multi-class problem equally well. The direct approach to feature normalization through the hard normalization operation results in a non-convex formulation. Instead, Ring loss applies soft normalization, where it gradually learns to constrain the norm to the scaled unit circle while preserving convexity leading to more robust features. We apply Ring loss to large-scale face recognition problems and present results on LFW, the challenging protocols of IJB-A Janus, Janus CS3 (a superset of IJB-A Janus), Celebrity Frontal-Profile (CFP) and MegaFace with 1 million distractors. Ring loss outperforms strong baselines, matches state-of-the-art performance on IJB-A Janus and outperforms all other results on the challenging Janus CS3 thereby achieving state-of-the-art. We also outperform strong baselines in handling extremely low resolution face matching.

Class Correlation affects Single Object Localization using Pre-trained ConvNets

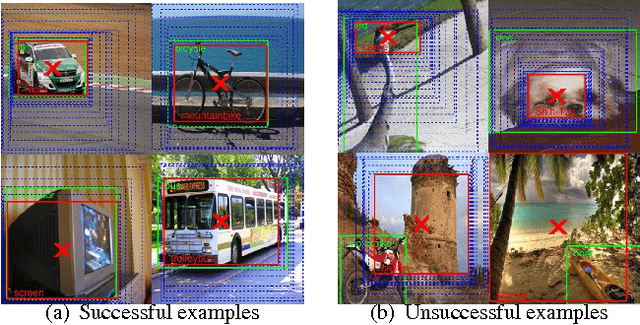
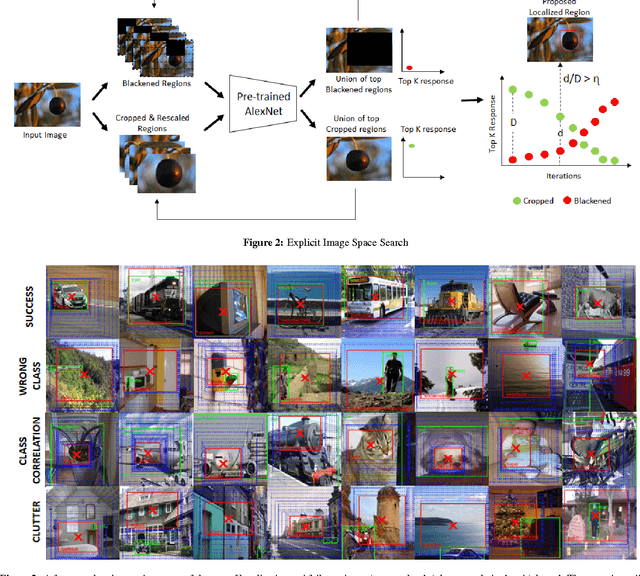
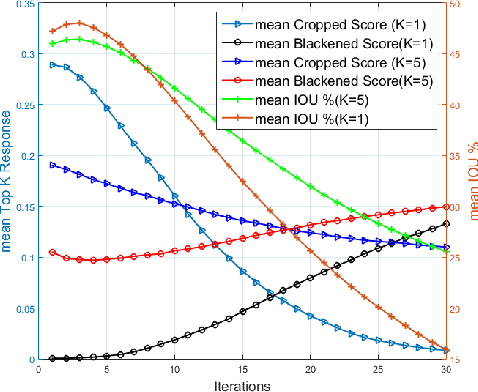
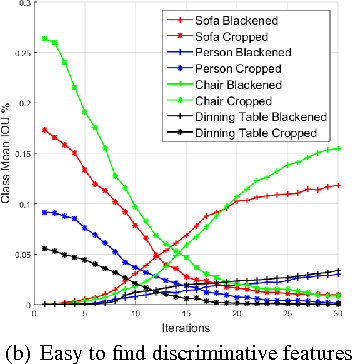
The problem of object localization has become one of the mainstream problems of vision. Most of the algorithms proposed involve the design for the model to be specifically for localizing objects. In this paper, we explore whether a pre-trained canonical ConvNet (without fine-tuning) trained purely for object classification on one dataset with global image level labels can be used to localize objects in images containing a single instance on a separate dataset while generalizing to novel classes. We propose a simple algorithm involving cropping and blackening out regions in the image space called Explicit Image Space based Search (EISS) for locating the most responsive regions in an image in the context of object localization. EISS brings to light the interesting phenomenon of a ConvNets responding more to features within objects as opposed to object level descriptors, as the classes in the training data get more correlated (visually/semantically similar).

Max-Margin Invariant Features from Transformed Unlabeled Data

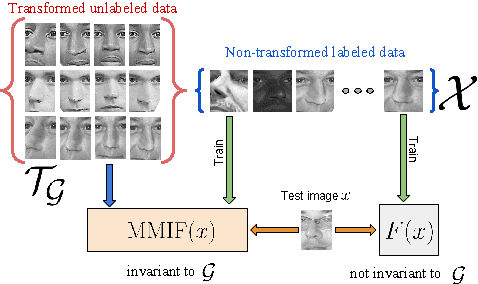
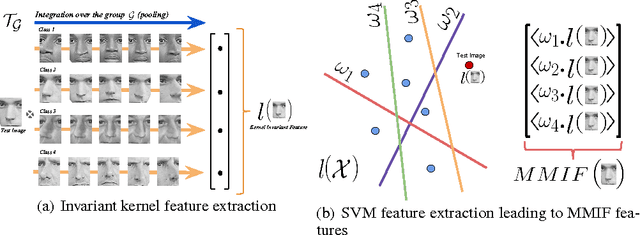
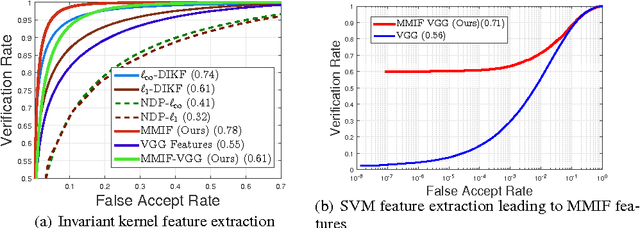
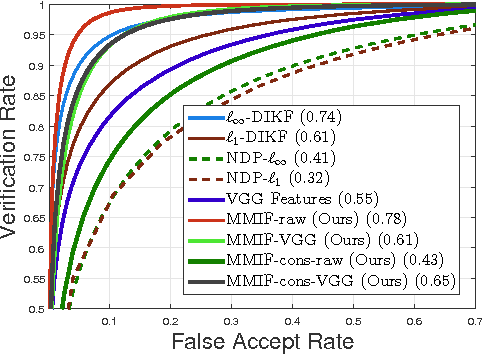
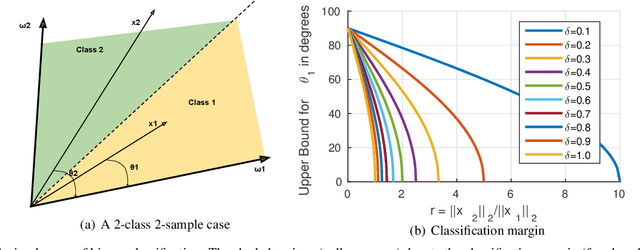
The study of representations invariant to common transformations of the data is important to learning. Most techniques have focused on local approximate invariance implemented within expensive optimization frameworks lacking explicit theoretical guarantees. In this paper, we study kernels that are invariant to a unitary group while having theoretical guarantees in addressing the important practical issue of unavailability of transformed versions of labelled data. A problem we call the Unlabeled Transformation Problem which is a special form of semi-supervised learning and one-shot learning. We present a theoretically motivated alternate approach to the invariant kernel SVM based on which we propose Max-Margin Invariant Features (MMIF) to solve this problem. As an illustration, we design an framework for face recognition and demonstrate the efficacy of our approach on a large scale semi-synthetic dataset with 153,000 images and a new challenging protocol on Labelled Faces in the Wild (LFW) while out-performing strong baselines.

How ConvNets model Non-linear Transformations

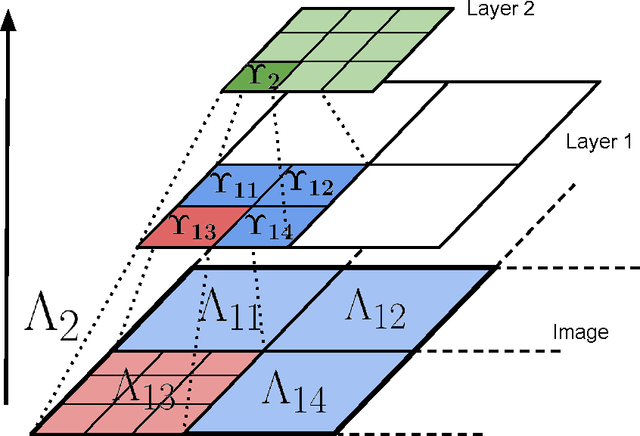
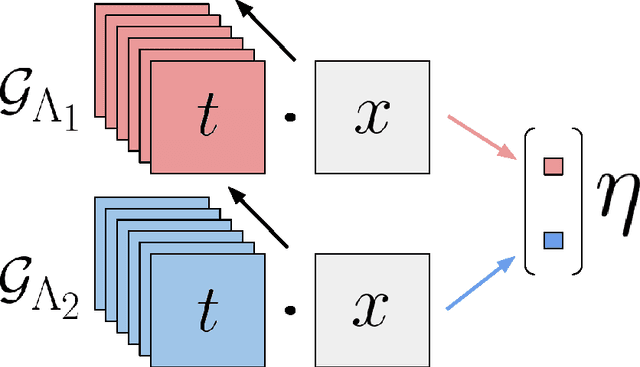
In this paper, we theoretically address three fundamental problems involving deep convolutional networks regarding invariance, depth and hierarchy. We introduce the paradigm of Transformation Networks (TN) which are a direct generalization of Convolutional Networks (ConvNets). Theoretically, we show that TNs (and thereby ConvNets) are can be invariant to non-linear transformations of the input despite pooling over mere local translations. Our analysis provides clear insights into the increase in invariance with depth in these networks. Deeper networks are able to model much richer classes of transformations. We also find that a hierarchical architecture allows the network to generate invariance much more efficiently than a non-hierarchical network. Our results provide useful insight into these three fundamental problems in deep learning using ConvNets.

Emergence of Selective Invariance in Hierarchical Feed Forward Networks

Many theories have emerged which investigate how in- variance is generated in hierarchical networks through sim- ple schemes such as max and mean pooling. The restriction to max/mean pooling in theoretical and empirical studies has diverted attention away from a more general way of generating invariance to nuisance transformations. We con- jecture that hierarchically building selective invariance (i.e. carefully choosing the range of the transformation to be in- variant to at each layer of a hierarchical network) is im- portant for pattern recognition. We utilize a novel pooling layer called adaptive pooling to find linear pooling weights within networks. These networks with the learnt pooling weights have performances on object categorization tasks that are comparable to max/mean pooling networks. In- terestingly, adaptive pooling can converge to mean pooling (when initialized with random pooling weights), find more general linear pooling schemes or even decide not to pool at all. We illustrate the general notion of selective invari- ance through object categorization experiments on large- scale datasets such as SVHN and ILSVRC 2012.

Unitary-Group Invariant Kernels and Features from Transformed Unlabeled Data

The study of representations invariant to common transformations of the data is important to learning. Most techniques have focused on local approximate invariance implemented within expensive optimization frameworks lacking explicit theoretical guarantees. In this paper, we study kernels that are invariant to the unitary group while having theoretical guarantees in addressing practical issues such as (1) unavailability of transformed versions of labelled data and (2) not observing all transformations. We present a theoretically motivated alternate approach to the invariant kernel SVM. Unlike previous approaches to the invariant SVM, the proposed formulation solves both issues mentioned. We also present a kernel extension of a recent technique to extract linear unitary-group invariant features addressing both issues and extend some guarantees regarding invariance and stability. We present experiments on the UCI ML datasets to illustrate and validate our methods.