Near-Field ISAC in 6G: Addressing Phase Nonlinearity via Lifted Super-Resolution

Integrated sensing and communications (ISAC) is a promising component of 6G networks, fusing communication and radar technologies to facilitate new services. Additionally, the use of extremely large-scale antenna arrays (ELLA) at the ISAC common receiver not only facilitates terahertz-rate communication links but also significantly enhances the accuracy of target detection in radar applications. In practical scenarios, communication scatterers and radar targets often reside in close proximity to the ISAC receiver. This, combined with the use of ELLA, fundamentally alters the electromagnetic characteristics of wireless and radar channels, shifting from far-field planar-wave propagation to near-field spherical wave propagation. Under the far-field planar-wave model, the phase of the array response vector varies linearly with the antenna index. In contrast, in the near-field spherical wave model, this phase relationship becomes nonlinear. This shift presents a fundamental challenge: the widely-used Fourier analysis can no longer be directly applied for target detection and communication channel estimation at the ISAC common receiver. In this work, we propose a feasible solution to address this fundamental issue. Specifically, we demonstrate that there exists a high-dimensional space in which the phase nonlinearity can be expressed as linear. Leveraging this insight, we develop a lifted super-resolution framework that simultaneously performs communication channel estimation and extracts target parameters with high precision.

Subspace-Informed Matrix Completion

In this work, we consider the matrix completion problem, where the objective is to reconstruct a low-rank matrix from a few observed entries. A commonly employed approach involves nuclear norm minimization. For this method to succeed, the number of observed entries needs to scale at least proportional to both the rank of the ground-truth matrix and the coherence parameter. While the only prior information is oftentimes the low-rank nature of the ground-truth matrix, in various real-world scenarios, additional knowledge about the ground-truth low-rank matrix is available. For instance, in collaborative filtering, Netflix problem, and dynamic channel estimation in wireless communications, we have partial or full knowledge about the signal subspace in advance. Specifically, we are aware of some subspaces that form multiple angles with the column and row spaces of the ground-truth matrix. Leveraging this valuable information has the potential to significantly reduce the required number of observations. To this end, we introduce a multi-weight nuclear norm optimization problem that concurrently promotes the low-rank property as well the information about the available subspaces. The proposed weights are tailored to penalize each angle corresponding to each basis of the prior subspace independently. We further propose an optimal weight selection strategy by minimizing the coherence parameter of the ground-truth matrix, which is equivalent to minimizing the required number of observations. Simulation results validate the advantages of incorporating multiple weights in the completion procedure. Specifically, our proposed multi-weight optimization problem demonstrates a substantial reduction in the required number of observations compared to the state-of-the-art methods.

Improved Downlink Channel Estimation in Time-Varying FDD Massive MIMO Systems

In this work, we address the challenge of accurately obtaining channel state information at the transmitter (CSIT) for frequency division duplexing (FDD) multiple input multiple output systems. Although CSIT is vital for maximizing spatial multiplexing gains, traditional CSIT estimation methods often suffer from impracticality due to the substantial training and feedback overhead they require. To address this challenge, we leverage two sources of prior information simultaneously: the presence of limited local scatterers at the base station (BS) and the time-varying characteristics of the channel. The former results in a redundant angular sparsity of users' channels exceeding the spatial dimension (i.e., the number of BS antennas), while the latter provides a prior non-uniform distribution in the angular domain. We propose a weighted optimization framework that simultaneously reflects both of these features. The optimal weights are then obtained by minimizing the expected recovery error of the optimization problem. This establishes an analytical closed-form relationship between the optimal weights and the angular domain characteristics. Numerical experiments verify the effectiveness of our proposed approach in reducing the recovery error and consequently resulting in decreased training and feedback overhead.

Optimal Transmitter Design and Pilot Spacing in MIMO Non-Stationary Aging Channels

This work considers an uplink wireless communication system where multiple users with multiple antennas transmit data frames over dynamic channels. Previous studies have shown that multiple transmit and receive antennas can substantially enhance the sum-capacity of all users when the channel is known at the transmitter and in the case of uncorrelated transmit and receive antennas. However, spatial correlations stemming from close proximity of transmit antennas and channel variation between pilot and data time slots, known as channel aging, can substantially degrade the transmission rate if they are not properly into account. In this work, we provide an analytical framework to concurrently exploit both of these features. Specifically, we first propose a beamforming framework to capture spatial correlations. Then, based on random matrix theory tools, we introduce a deterministic expression that approximates the average sum-capacity of all users. Subsequently, we obtain the optimal values of pilot spacing and beamforming vectors upon maximizing this expression. Simulation results show the impacts of path loss, velocity of mobile users and Rician factor on the resulting sum-capacity and underscore the efficacy of our methodology compared to prior works.

Exploiting Spatial and Temporal Correlations in Massive MIMO Systems Over Non-Stationary Aging Channels

This work investigates a multi-user, multi-antenna uplink wireless system, where multiple users transmit signals to a base station. Previous research has explored the potential for linear growth in spectral efficiency by employing multiple transmit and receive antennas. This gain depends on the quality of channel state information and uncorrelated antennas. However, spatial correlations, arising from closely-spaced antennas, and channel aging effects, stemming from the difference between the channel at pilot and data time instances, can substantially counteract these benefits and degrade the transmission rate, especially in non-stationary environments. To address these challenges, this work introduces a real-time beamforming framework to compensate for the spatial correlation effect. A channel estimation scheme is then developed, leveraging temporal channel correlations and considering mobile device velocity and antenna spacing. Subsequently, an expression approximating the average spectral efficiency is obtained, dependent on pilot spacing, pilot and data powers, and beamforming vectors. By maximizing this expression, optimal parameters are identified. Numerical results reveal the effectiveness of the proposed approach compared to prior works. Moreover, optimal pilot spacing remains unaffected by interference components such as path loss and the velocity of interference users. The impact of interference components also diminishes with an increasing number of transmit antennas.

Towards Optimal Pilot Spacing and Power Control in Multi-Antenna Systems Operating Over Non-Stationary Rician Aging Channels

Several previous works have addressed the inherent trade-off between allocating resources in the power and time domains to pilot and data signals in multiple input multiple output systems over block-fading channels. In particular, when the channel changes rapidly in time, channel aging degrades the performance in terms of spectral efficiency without proper pilot spacing and power control. Despite recognizing non-stationary stochastic processes as more accurate models for time-varying wireless channels, the problem of pilot spacing and power control in multi-antenna systems operating over non-stationary channels is not addressed in the literature. In this paper, we address this gap by introducing a refined first-order autoregressive model that exploits the inherent temporal correlations over non-stationary Rician aging channels. We design a multi-frame structure for data transmission that better reflects the non-stationary fading environment than previously developed single-frame structures. Subsequently, to determine optimal pilot spacing and power control within this multi-frame structure, we develop an optimization framework and an efficient algorithm based on maximizing a deterministic equivalent expression for the spectral efficiency, demonstrating its generality by encompassing previous channel aging results. Our numerical results indicate the efficacy of the proposed method in terms of spectral efficiency gains over the single frame structure.

Off-the-grid Blind Deconvolution and Demixing

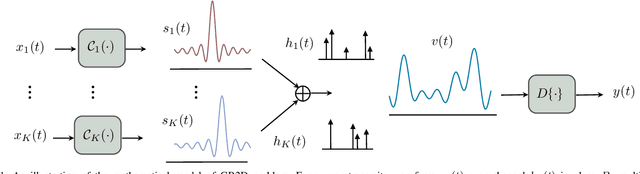
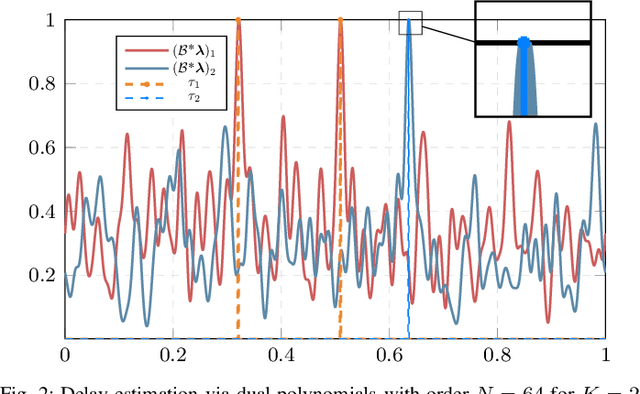
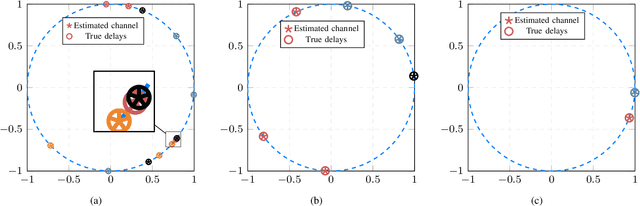
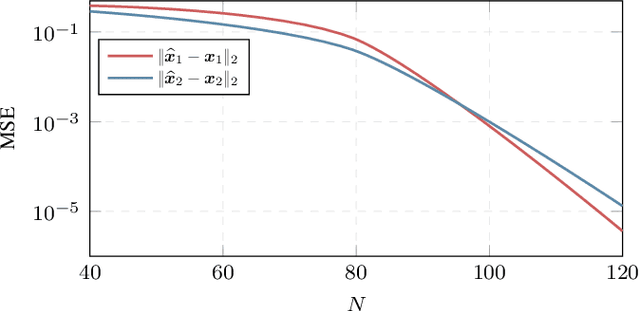
We consider the problem of gridless blind deconvolution and demixing (GB2D) in scenarios where multiple users communicate messages through multiple unknown channels, and a single base station (BS) collects their contributions. This scenario arises in various communication fields, including wireless communications, the Internet of Things, over-the-air computation, and integrated sensing and communications. In this setup, each user's message is convolved with a multi-path channel formed by several scaled and delayed copies of Dirac spikes. The BS receives a linear combination of the convolved signals, and the goal is to recover the unknown amplitudes, continuous-indexed delays, and transmitted waveforms from a compressed vector of measurements at the BS. However, in the absence of any prior knowledge of the transmitted messages and channels, GB2D is highly challenging and intractable in general. To address this issue, we assume that each user's message follows a distinct modulation scheme living in a known low-dimensional subspace. By exploiting these subspace assumptions and the sparsity of the multipath channels for different users, we transform the nonlinear GB2D problem into a matrix tuple recovery problem from a few linear measurements. To achieve this, we propose a semidefinite programming optimization that exploits the specific low-dimensional structure of the matrix tuple to recover the messages and continuous delays of different communication paths from a single received signal at the BS. Finally, our numerical experiments show that our proposed method effectively recovers all transmitted messages and the continuous delay parameters of the channels with a sufficient number of samples.

Blind Asynchronous Goal-Oriented Detection for Massive Connectivity

Resource allocation and multiple access schemes are instrumental for the success of communication networks, which facilitate seamless wireless connectivity among a growing population of uncoordinated and non-synchronized users. In this paper, we present a novel random access scheme that addresses one of the most severe barriers of current strategies to achieve massive connectivity and ultra-reliable and low latency communications for 6G. The proposed scheme utilizes wireless channels' angular continuous group-sparsity feature to provide low latency, high reliability, and massive access features in the face of limited time-bandwidth resources, asynchronous transmissions, and preamble errors. Specifically, a reconstruction-free goal-oriented optimization problem is proposed, which preserves the angular information of active devices and is then complemented by a clustering algorithm to assign active users to specific groups. This allows us to identify active stationary devices according to their line of sight angles. Additionally, for mobile devices, an alternating minimization algorithm is proposed to recover their preamble, data, and channel gains simultaneously, enabling the identification of active mobile users. Simulation results show that the proposed algorithm provides excellent performance and supports a massive number of devices. Moreover, the performance of the proposed scheme is independent of the total number of devices, distinguishing it from other random access schemes. The proposed method provides a unified solution to meet the requirements of machine-type communications and ultra-reliable and low-latency communications, making it an important contribution to the emerging 6G networks.

Multi-User Distributed Computing Via Compressed Sensing

The multi-user linearly-separable distributed computing problem is considered here, in which $N$ servers help to compute the real-valued functions requested by $K$ users, where each function can be written as a linear combination of up to $L$ (generally non-linear) subfunctions. Each server computes a fraction $\gamma$ of the subfunctions, then communicates a function of its computed outputs to some of the users, and then each user collects its received data to recover its desired function. Our goal is to bound the ratio between the computation workload done by all servers over the number of datasets. To this end, we here reformulate the real-valued distributed computing problem into a matrix factorization problem and then into a basic sparse recovery problem, where sparsity implies computational savings. Building on this, we first give a simple probabilistic scheme for subfunction assignment, which allows us to upper bound the optimal normalized computation cost as $\gamma \leq \frac{K}{N}$ that a generally intractable $\ell_0$-minimization would give. To bypass the intractability of such optimal scheme, we show that if these optimal schemes enjoy $\gamma \leq - r\frac{K}{N}W^{-1}_{-1}(- \frac{2K}{e N r} )$ (where $W_{-1}(\cdot)$ is the Lambert function and $r$ calibrates the communication between servers and users), then they can actually be derived using a tractable Basis Pursuit $\ell_1$-minimization. This newly-revealed connection between distributed computation and compressed sensing opens up the possibility of designing practical distributed computing algorithms by employing tools and methods from compressed sensing.

Distribution-aware $\ell_1$ Analysis Minimization

This work is about recovering an analysis-sparse vector, i.e. sparse vector in some transform domain, from under-sampled measurements. In real-world applications, there often exist random analysis-sparse vectors whose distribution in the analysis domain are known. To exploit this information, a weighted $\ell_1$ analysis minimization is often considered. The task of choosing the weights in this case is however challenging and non-trivial. In this work, we provide an analytical method to choose the suitable weights. Specifically, we first obtain a tight upper-bound expression for the expected number of required measurements. This bound depends on two critical parameters: support distribution and expected sign of the analysis domain which are both accessible in advance. Then, we calculate the near-optimal weights by minimizing this expression with respect to the weights. Our strategy works for both noiseless and noisy settings. Numerical results demonstrate the superiority of our proposed method. Specifically, the weighted $\ell_1$ analysis minimization with our near-optimal weighting design considerably needs fewer measurements than its regular $\ell_1$ analysis counterpart.