Off-the-grid Blind Deconvolution and Demixing
Paper and Code
Aug 07, 2023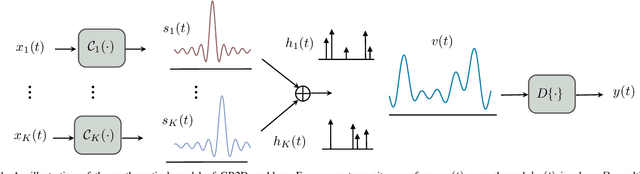
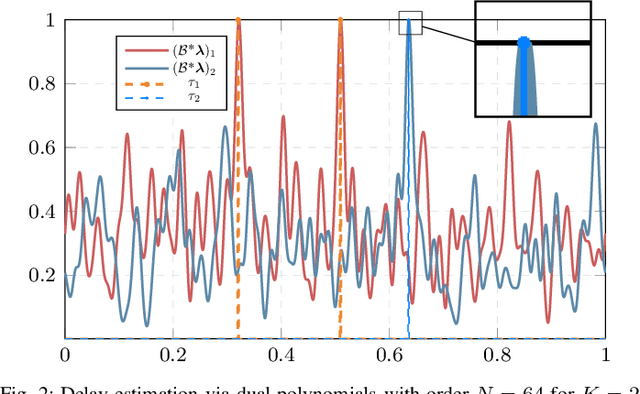
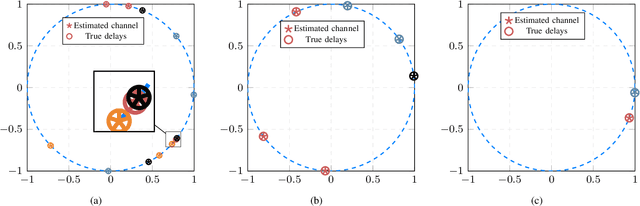
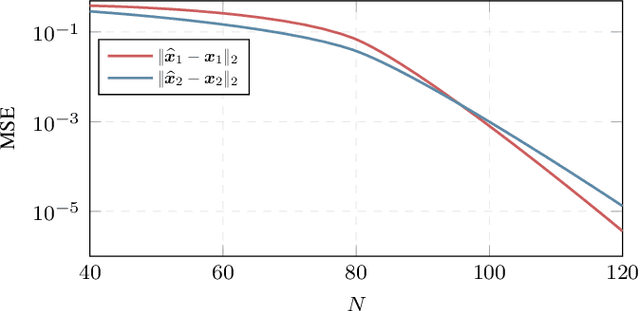
We consider the problem of gridless blind deconvolution and demixing (GB2D) in scenarios where multiple users communicate messages through multiple unknown channels, and a single base station (BS) collects their contributions. This scenario arises in various communication fields, including wireless communications, the Internet of Things, over-the-air computation, and integrated sensing and communications. In this setup, each user's message is convolved with a multi-path channel formed by several scaled and delayed copies of Dirac spikes. The BS receives a linear combination of the convolved signals, and the goal is to recover the unknown amplitudes, continuous-indexed delays, and transmitted waveforms from a compressed vector of measurements at the BS. However, in the absence of any prior knowledge of the transmitted messages and channels, GB2D is highly challenging and intractable in general. To address this issue, we assume that each user's message follows a distinct modulation scheme living in a known low-dimensional subspace. By exploiting these subspace assumptions and the sparsity of the multipath channels for different users, we transform the nonlinear GB2D problem into a matrix tuple recovery problem from a few linear measurements. To achieve this, we propose a semidefinite programming optimization that exploits the specific low-dimensional structure of the matrix tuple to recover the messages and continuous delays of different communication paths from a single received signal at the BS. Finally, our numerical experiments show that our proposed method effectively recovers all transmitted messages and the continuous delay parameters of the channels with a sufficient number of samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge