Compositional Estimation of Lipschitz Constants for Deep Neural Networks

The Lipschitz constant plays a crucial role in certifying the robustness of neural networks to input perturbations and adversarial attacks, as well as the stability and safety of systems with neural network controllers. Therefore, estimation of tight bounds on the Lipschitz constant of neural networks is a well-studied topic. However, typical approaches involve solving a large matrix verification problem, the computational cost of which grows significantly for deeper networks. In this letter, we provide a compositional approach to estimate Lipschitz constants for deep feedforward neural networks by obtaining an exact decomposition of the large matrix verification problem into smaller sub-problems. We further obtain a closed-form solution that applies to most common neural network activation functions, which will enable rapid robustness and stability certificates for neural networks deployed in online control settings. Finally, we demonstrate through numerical experiments that our approach provides a steep reduction in computation time while yielding Lipschitz bounds that are very close to those achieved by state-of-the-art approaches.

Sampling-based Safe Reinforcement Learning for Nonlinear Dynamical Systems

We develop provably safe and convergent reinforcement learning (RL) algorithms for control of nonlinear dynamical systems, bridging the gap between the hard safety guarantees of control theory and the convergence guarantees of RL theory. Recent advances at the intersection of control and RL follow a two-stage, safety filter approach to enforcing hard safety constraints: model-free RL is used to learn a potentially unsafe controller, whose actions are projected onto safe sets prescribed, for example, by a control barrier function. Though safe, such approaches lose any convergence guarantees enjoyed by the underlying RL methods. In this paper, we develop a single-stage, sampling-based approach to hard constraint satisfaction that learns RL controllers enjoying classical convergence guarantees while satisfying hard safety constraints throughout training and deployment. We validate the efficacy of our approach in simulation, including safe control of a quadcopter in a challenging obstacle avoidance problem, and demonstrate that it outperforms existing benchmarks.

Learning Dissipative Neural Dynamical Systems

Consider an unknown nonlinear dynamical system that is known to be dissipative. The objective of this paper is to learn a neural dynamical model that approximates this system, while preserving the dissipativity property in the model. In general, imposing dissipativity constraints during neural network training is a hard problem for which no known techniques exist. In this work, we address the problem of learning a dissipative neural dynamical system model in two stages. First, we learn an unconstrained neural dynamical model that closely approximates the system dynamics. Next, we derive sufficient conditions to perturb the weights of the neural dynamical model to ensure dissipativity, followed by perturbation of the biases to retain the fit of the model to the trajectories of the nonlinear system. We show that these two perturbation problems can be solved independently to obtain a neural dynamical model that is guaranteed to be dissipative while closely approximating the nonlinear system.

Distributed Learning of Neural Lyapunov Functions for Large-Scale Networked Dissipative Systems

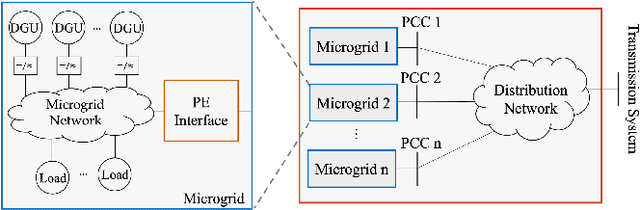
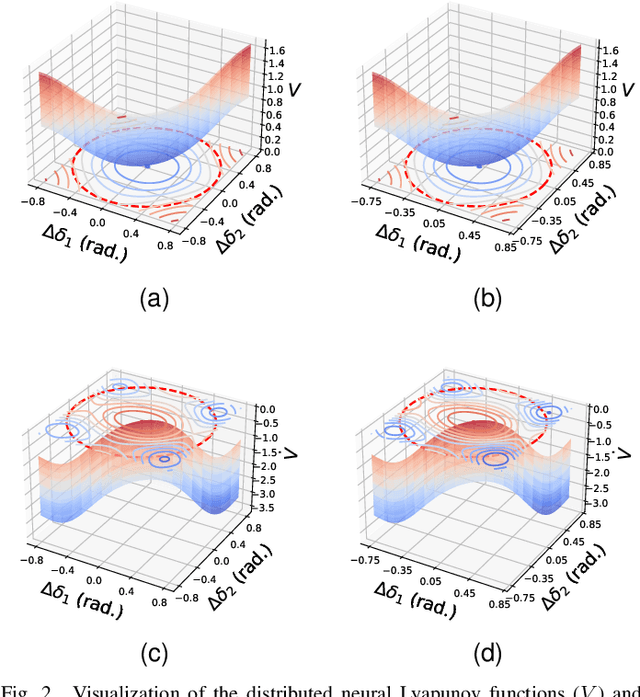
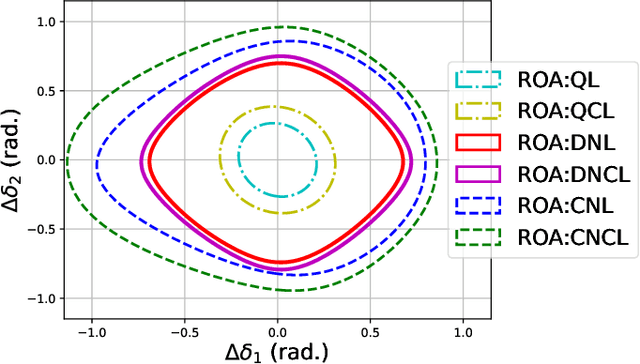
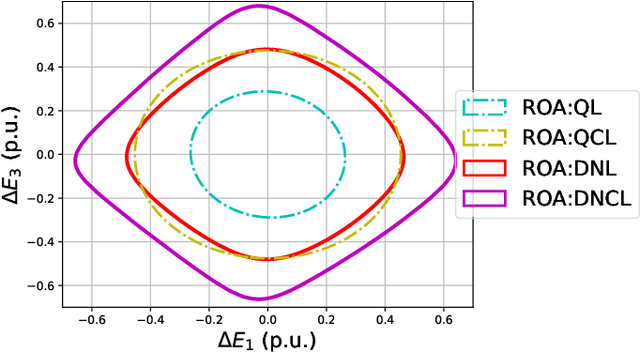
This paper considers the problem of characterizing the stability region of a large-scale networked system comprised of dissipative nonlinear subsystems, in a distributed and computationally tractable way. One standard approach to estimate the stability region of a general nonlinear system is to first find a Lyapunov function for the system and characterize its region of attraction as the stability region. However, classical approaches, such as sum-of-squares methods and quadratic approximation, for finding a Lyapunov function either do not scale to large systems or give very conservative estimates for the stability region. In this context, we propose a new distributed learning based approach by exploiting the dissipativity structure of the subsystems. Our approach has two parts: the first part is a distributed approach to learn the storage functions (similar to the Lyapunov functions) for all the subsystems, and the second part is a distributed optimization approach to find the Lyapunov function for the networked system using the learned storage functions of the subsystems. We demonstrate the superior performance of our proposed approach through extensive case studies in microgrid networks.

PSML: A Multi-scale Time-series Dataset for Machine Learning in Decarbonized Energy Grids

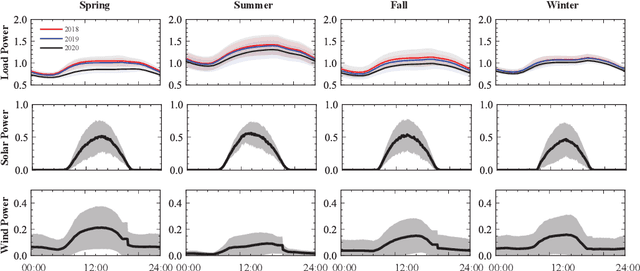
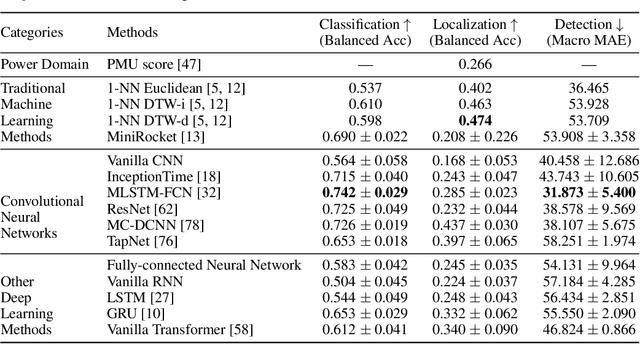
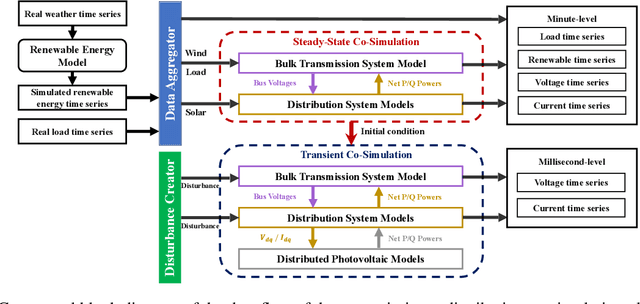
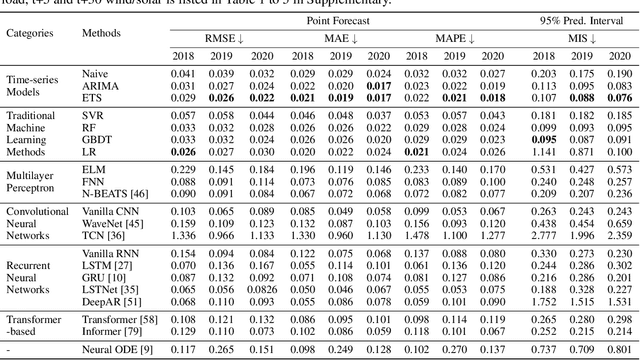
The electric grid is a key enabling infrastructure for the ambitious transition towards carbon neutrality as we grapple with climate change. With deepening penetration of renewable energy resources and electrified transportation, the reliable and secure operation of the electric grid becomes increasingly challenging. In this paper, we present PSML, a first-of-its-kind open-access multi-scale time-series dataset, to aid in the development of data-driven machine learning (ML) based approaches towards reliable operation of future electric grids. The dataset is generated through a novel transmission + distribution (T+D) co-simulation designed to capture the increasingly important interactions and uncertainties of the grid dynamics, containing electric load, renewable generation, weather, voltage and current measurements at multiple spatio-temporal scales. Using PSML, we provide state-of-the-art ML baselines on three challenging use cases of critical importance to achieve: (i) early detection, accurate classification and localization of dynamic disturbance events; (ii) robust hierarchical forecasting of load and renewable energy with the presence of uncertainties and extreme events; and (iii) realistic synthetic generation of physical-law-constrained measurement time series. We envision that this dataset will enable advances for ML in dynamic systems, while simultaneously allowing ML researchers to contribute towards carbon-neutral electricity and mobility.