Distributed Learning of Neural Lyapunov Functions for Large-Scale Networked Dissipative Systems
Paper and Code
Jul 15, 2022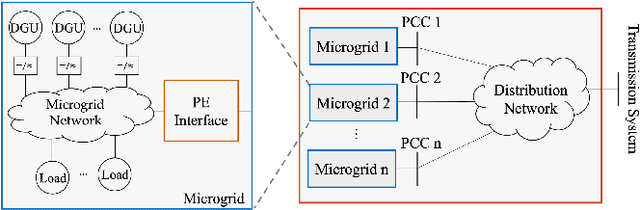
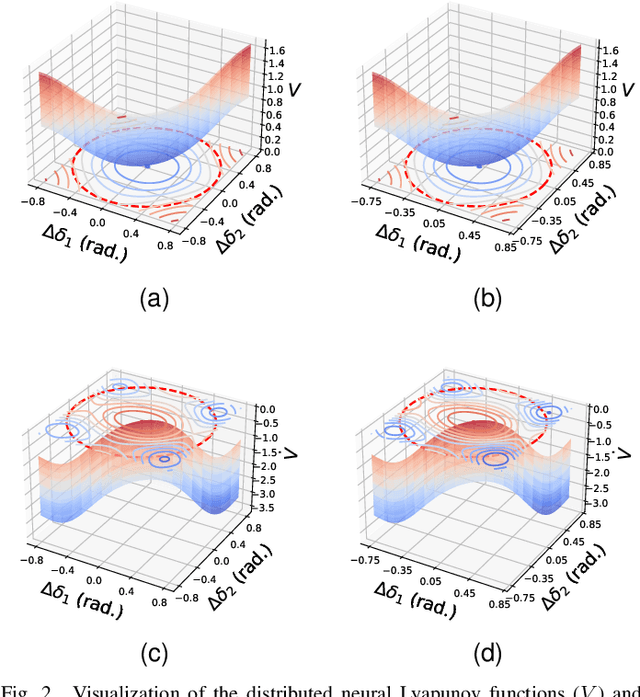
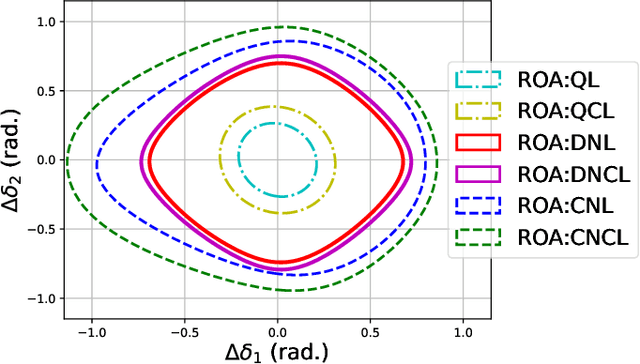
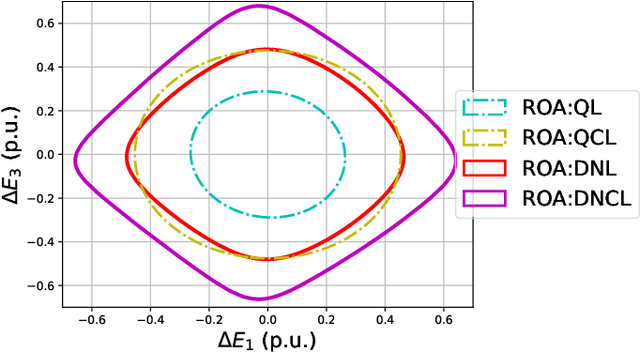
This paper considers the problem of characterizing the stability region of a large-scale networked system comprised of dissipative nonlinear subsystems, in a distributed and computationally tractable way. One standard approach to estimate the stability region of a general nonlinear system is to first find a Lyapunov function for the system and characterize its region of attraction as the stability region. However, classical approaches, such as sum-of-squares methods and quadratic approximation, for finding a Lyapunov function either do not scale to large systems or give very conservative estimates for the stability region. In this context, we propose a new distributed learning based approach by exploiting the dissipativity structure of the subsystems. Our approach has two parts: the first part is a distributed approach to learn the storage functions (similar to the Lyapunov functions) for all the subsystems, and the second part is a distributed optimization approach to find the Lyapunov function for the networked system using the learned storage functions of the subsystems. We demonstrate the superior performance of our proposed approach through extensive case studies in microgrid networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge