GraphScale: A Framework to Enable Machine Learning over Billion-node Graphs

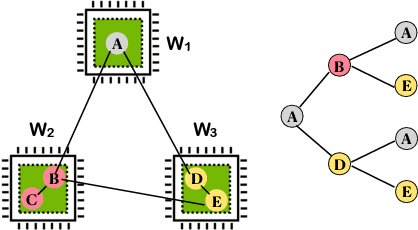
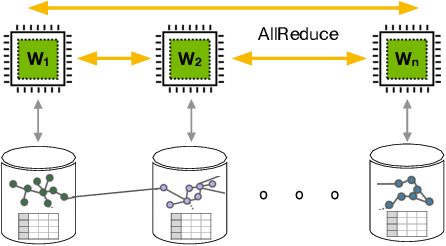
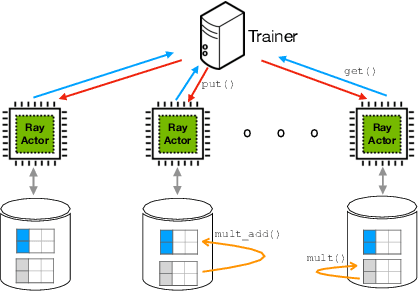
Graph Neural Networks (GNNs) have emerged as powerful tools for supervised machine learning over graph-structured data, while sampling-based node representation learning is widely utilized in unsupervised learning. However, scalability remains a major challenge in both supervised and unsupervised learning for large graphs (e.g., those with over 1 billion nodes). The scalability bottleneck largely stems from the mini-batch sampling phase in GNNs and the random walk sampling phase in unsupervised methods. These processes often require storing features or embeddings in memory. In the context of distributed training, they require frequent, inefficient random access to data stored across different workers. Such repeated inter-worker communication for each mini-batch leads to high communication overhead and computational inefficiency. We propose GraphScale, a unified framework for both supervised and unsupervised learning to store and process large graph data distributedly. The key insight in our design is the separation of workers who store data and those who perform the training. This separation allows us to decouple computing and storage in graph training, thus effectively building a pipeline where data fetching and data computation can overlap asynchronously. Our experiments show that GraphScale outperforms state-of-the-art methods for distributed training of both GNNs and node embeddings. We evaluate GraphScale both on public and proprietary graph datasets and observe a reduction of at least 40% in end-to-end training times compared to popular distributed frameworks, without any loss in performance. While most existing methods don't support billion-node graphs for training node embeddings, GraphScale is currently deployed in production at TikTok enabling efficient learning over such large graphs.

SAS+ Planning as Satisfiability

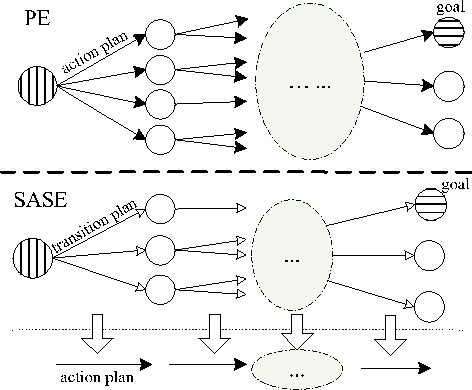
Planning as satisfiability is a principal approach to planning with many eminent advantages. The existing planning as satisfiability techniques usually use encodings compiled from STRIPS. We introduce a novel SAT encoding scheme (SASE) based on the SAS+ formalism. The new scheme exploits the structural information in SAS+, resulting in an encoding that is both more compact and efficient for planning. We prove the correctness of the new encoding by establishing an isomorphism between the solution plans of SASE and that of STRIPS based encodings. We further analyze the transition variables newly introduced in SASE to explain why it accommodates modern SAT solving algorithms and improves performance. We give empirical statistical results to support our analysis. We also develop a number of techniques to further reduce the encoding size of SASE, and conduct experimental studies to show the strength of each individual technique. Finally, we report extensive experimental results to demonstrate significant improvements of SASE over the state-of-the-art STRIPS based encoding schemes in terms of both time and memory efficiency.

Theory and Algorithms for Partial Order Based Reduction in Planning

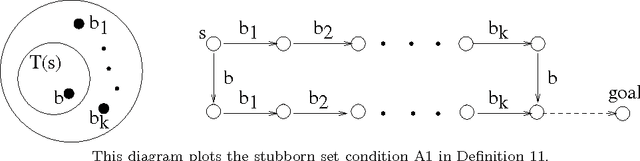
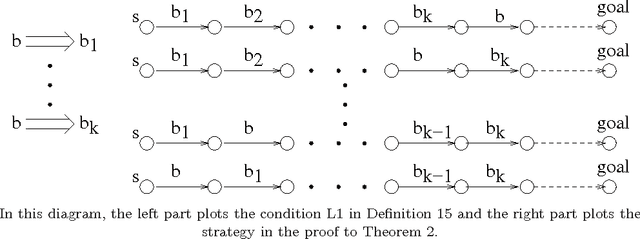
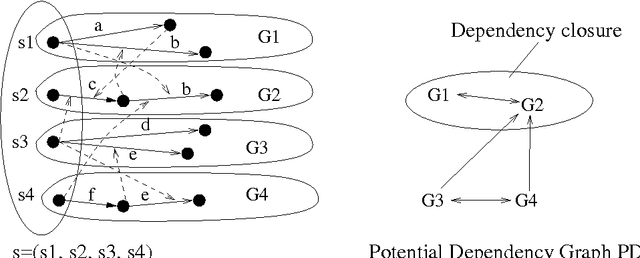
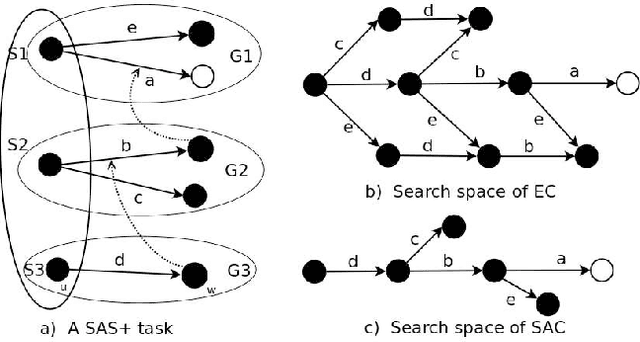
Search is a major technique for planning. It amounts to exploring a state space of planning domains typically modeled as a directed graph. However, prohibitively large sizes of the search space make search expensive. Developing better heuristic functions has been the main technique for improving search efficiency. Nevertheless, recent studies have shown that improving heuristics alone has certain fundamental limits on improving search efficiency. Recently, a new direction of research called partial order based reduction (POR) has been proposed as an alternative to improving heuristics. POR has shown promise in speeding up searches. POR has been extensively studied in model checking research and is a key enabling technique for scalability of model checking systems. Although the POR theory has been extensively studied in model checking, it has never been developed systematically for planning before. In addition, the conditions for POR in the model checking theory are abstract and not directly applicable in planning. Previous works on POR algorithms for planning did not establish the connection between these algorithms and existing theory in model checking. In this paper, we develop a theory for POR in planning. The new theory we develop connects the stubborn set theory in model checking and POR methods in planning. We show that previous POR algorithms in planning can be explained by the new theory. Based on the new theory, we propose a new, stronger POR algorithm. Experimental results on various planning domains show further search cost reduction using the new algorithm.