SAS+ Planning as Satisfiability
Paper and Code
Jan 18, 2014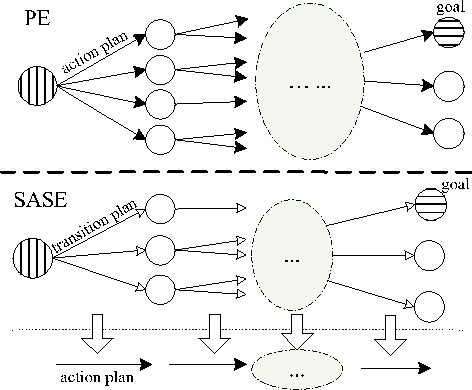



Planning as satisfiability is a principal approach to planning with many eminent advantages. The existing planning as satisfiability techniques usually use encodings compiled from STRIPS. We introduce a novel SAT encoding scheme (SASE) based on the SAS+ formalism. The new scheme exploits the structural information in SAS+, resulting in an encoding that is both more compact and efficient for planning. We prove the correctness of the new encoding by establishing an isomorphism between the solution plans of SASE and that of STRIPS based encodings. We further analyze the transition variables newly introduced in SASE to explain why it accommodates modern SAT solving algorithms and improves performance. We give empirical statistical results to support our analysis. We also develop a number of techniques to further reduce the encoding size of SASE, and conduct experimental studies to show the strength of each individual technique. Finally, we report extensive experimental results to demonstrate significant improvements of SASE over the state-of-the-art STRIPS based encoding schemes in terms of both time and memory efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge