Papaya: Practical, Private, and Scalable Federated Learning

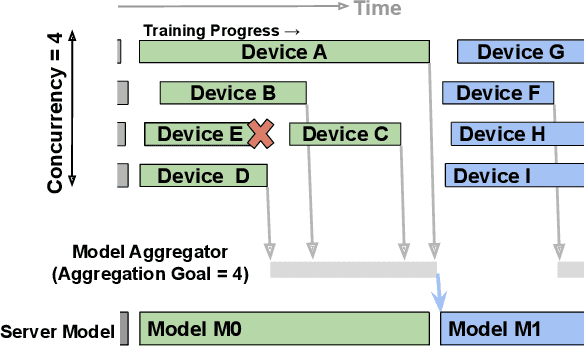
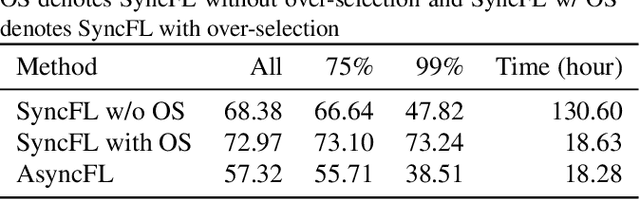
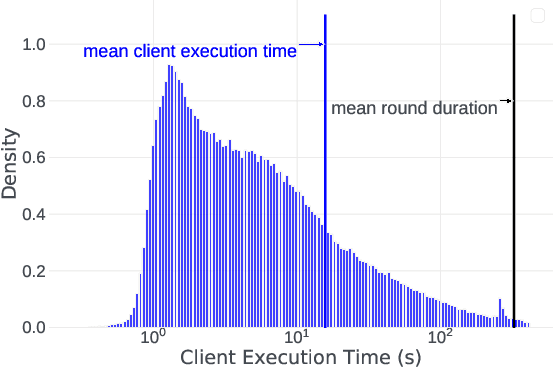
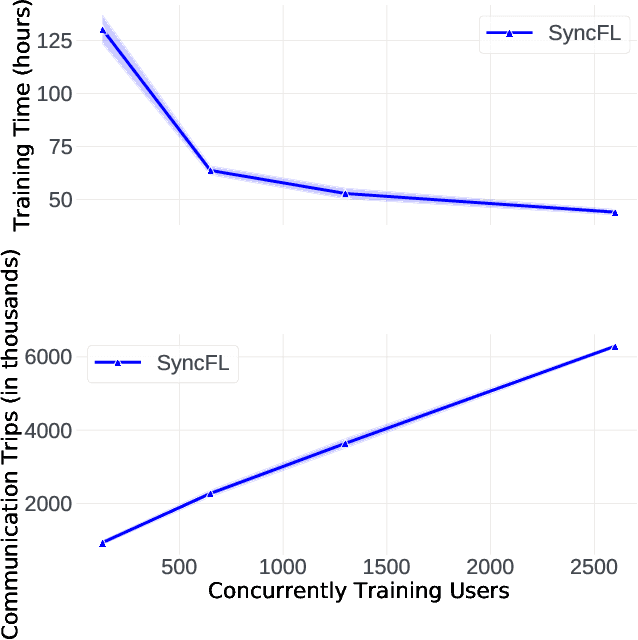
Cross-device Federated Learning (FL) is a distributed learning paradigm with several challenges that differentiate it from traditional distributed learning, variability in the system characteristics on each device, and millions of clients coordinating with a central server being primary ones. Most FL systems described in the literature are synchronous - they perform a synchronized aggregation of model updates from individual clients. Scaling synchronous FL is challenging since increasing the number of clients training in parallel leads to diminishing returns in training speed, analogous to large-batch training. Moreover, stragglers hinder synchronous FL training. In this work, we outline a production asynchronous FL system design. Our work tackles the aforementioned issues, sketches of some of the system design challenges and their solutions, and touches upon principles that emerged from building a production FL system for millions of clients. Empirically, we demonstrate that asynchronous FL converges faster than synchronous FL when training across nearly one hundred million devices. In particular, in high concurrency settings, asynchronous FL is 5x faster and has nearly 8x less communication overhead than synchronous FL.

Secure multiparty computations in floating-point arithmetic

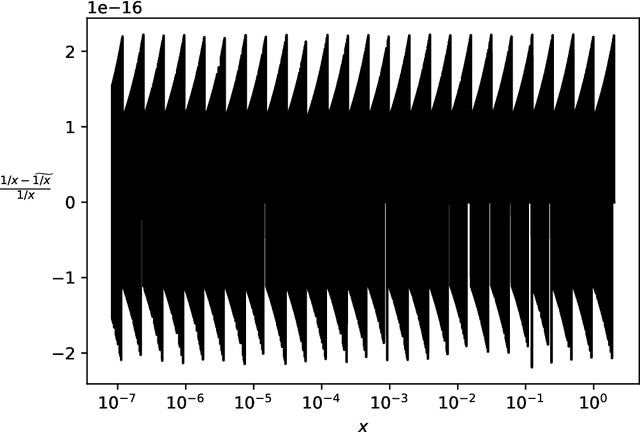
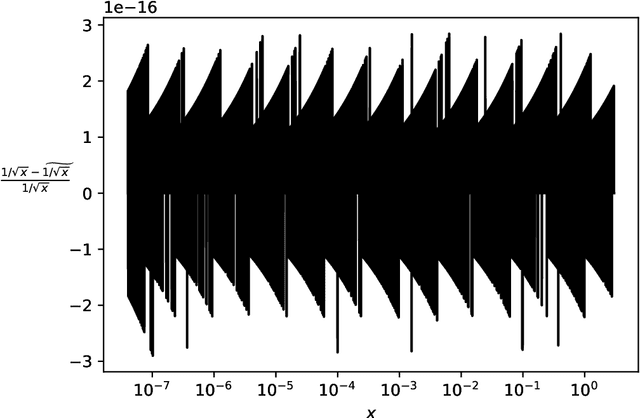
Secure multiparty computations enable the distribution of so-called shares of sensitive data to multiple parties such that the multiple parties can effectively process the data while being unable to glean much information about the data (at least not without collusion among all parties to put back together all the shares). Thus, the parties may conspire to send all their processed results to a trusted third party (perhaps the data provider) at the conclusion of the computations, with only the trusted third party being able to view the final results. Secure multiparty computations for privacy-preserving machine-learning turn out to be possible using solely standard floating-point arithmetic, at least with a carefully controlled leakage of information less than the loss of accuracy due to roundoff, all backed by rigorous mathematical proofs of worst-case bounds on information loss and numerical stability in finite-precision arithmetic. Numerical examples illustrate the high performance attained on commodity off-the-shelf hardware for generalized linear models, including ordinary linear least-squares regression, binary and multinomial logistic regression, probit regression, and Poisson regression.