A Local Approach to Forward Model Learning: Results on the Game of Life Game

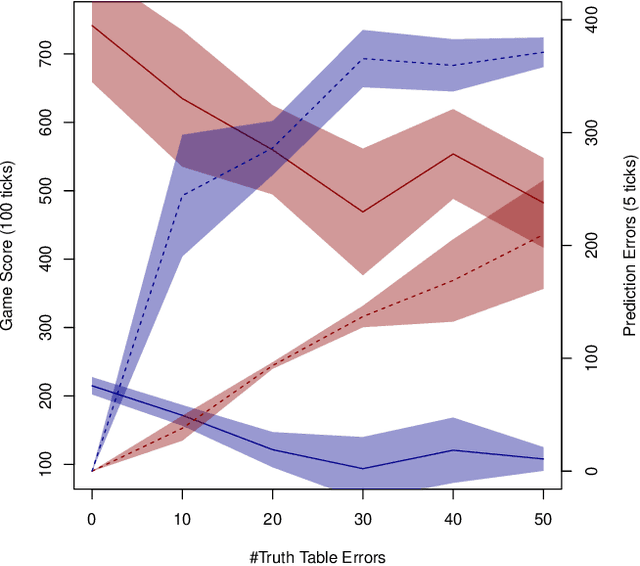
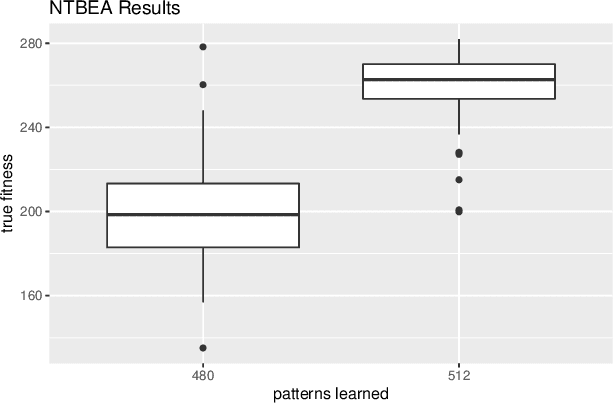
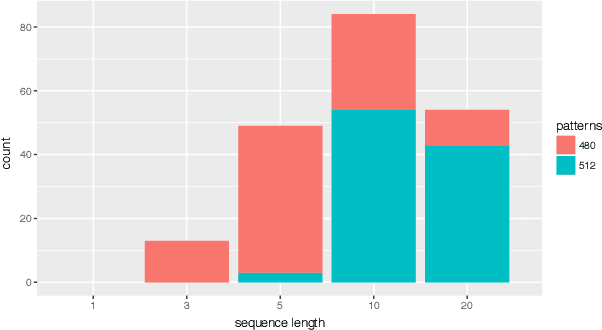
This paper investigates the effect of learning a forward model on the performance of a statistical forward planning agent. We transform Conway's Game of Life simulation into a single-player game where the objective can be either to preserve as much life as possible or to extinguish all life as quickly as possible. In order to learn the forward model of the game, we formulate the problem in a novel way that learns the local cell transition function by creating a set of supervised training data and predicting the next state of each cell in the grid based on its current state and immediate neighbours. Using this method we are able to harvest sufficient data to learn perfect forward models by observing only a few complete state transitions, using either a look-up table, a decision tree or a neural network. In contrast, learning the complete state transition function is a much harder task and our initial efforts to do this using deep convolutional auto-encoders were less successful. We also investigate the effects of imperfect learned models on prediction errors and game-playing performance, and show that even models with significant errors can provide good performance.

Reasoning with Mass Distributions

The concept of movable evidence masses that flow from supersets to subsets as specified by experts represents a suitable framework for reasoning under uncertainty. The mass flow is controlled by specialization matrices. New evidence is integrated into the frame of discernment by conditioning or revision (Dempster's rule of conditioning), for which special specialization matrices exist. Even some aspects of non-monotonic reasoning can be represented by certain specialization matrices.