Combined Pruning for Nested Cross-Validation to Accelerate Automated Hyperparameter Optimization for Embedded Feature Selection in High-Dimensional Data with Very Small Sample Sizes

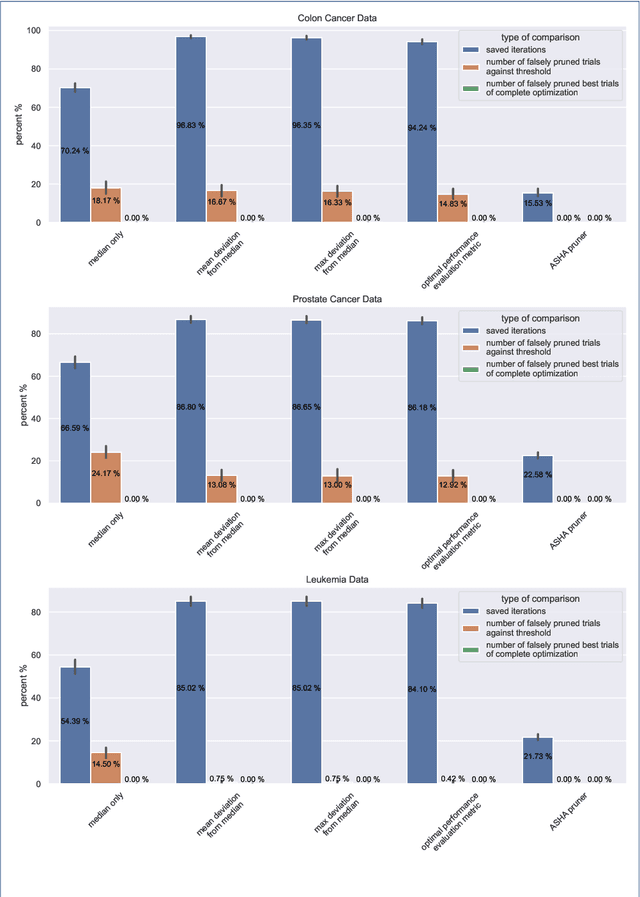
Applying tree-based embedded feature selection to exclude irrelevant features in high-dimensional data with very small sample sizes requires optimized hyperparameters for the model building process. In addition, nested cross-validation must be applied for this type of data to avoid biased model performance. The resulting long computation time can be accelerated with pruning. However, standard pruning algorithms must prune late or risk aborting calculations of promising hyperparameter sets due to high variance in the performance evaluation metric. To address this, we adapt the usage of a state-of-the-art successive halving pruner and combine it with two new pruning strategies based on domain or prior knowledge. One additional pruning strategy immediately stops the computation of trials with semantically meaningless results for the selected hyperparameter combinations. The other is an extrapolating threshold pruning strategy suitable for nested-cross-validation with high variance. Our proposed combined three-layer pruner keeps promising trials while reducing the number of models to be built by up to 81,3% compared to using a state-of-the-art asynchronous successive halving pruner alone. Our three-layer pruner implementation(available at https://github.com/sigrun-may/cv-pruner) speeds up data analysis or enables deeper hyperparameter search within the same computation time. It consequently saves time, money and energy, reducing the CO2 footprint.

Reasoning with Mass Distributions

The concept of movable evidence masses that flow from supersets to subsets as specified by experts represents a suitable framework for reasoning under uncertainty. The mass flow is controlled by specialization matrices. New evidence is integrated into the frame of discernment by conditioning or revision (Dempster's rule of conditioning), for which special specialization matrices exist. Even some aspects of non-monotonic reasoning can be represented by certain specialization matrices.

The Dynamic of Belief in the Transferable Belief Model and Specialization-Generalization Matrices

The fundamental updating process in the transferable belief model is related to the concept of specialization and can be described by a specialization matrix. The degree of belief in the truth of a proposition is a degree of justified support. The Principle of Minimal Commitment implies that one should never give more support to the truth of a proposition than justified. We show that Dempster's rule of conditioning corresponds essentially to the least committed specialization, and that Dempster's rule of combination results essentially from commutativity requirements. The concept of generalization, dual to thc concept of specialization, is described.