Flexible Decomposition Algorithms for Weakly Coupled Markov Decision Problems

This paper presents two new approaches to decomposing and solving large Markov decision problems (MDPs), a partial decoupling method and a complete decoupling method. In these approaches, a large, stochastic decision problem is divided into smaller pieces. The first approach builds a cache of policies for each part of the problem independently, and then combines the pieces in a separate, light-weight step. A second approach also divides the problem into smaller pieces, but information is communicated between the different problem pieces, allowing intelligent decisions to be made about which piece requires the most attention. Both approaches can be used to find optimal policies or approximately optimal policies with provable bounds. These algorithms also provide a framework for the efficient transfer of knowledge across problems that share similar structure.

Policy Iteration for Factored MDPs

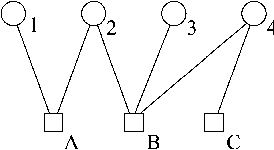
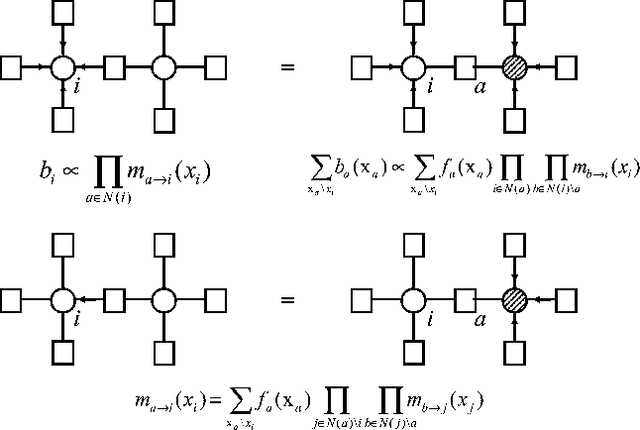
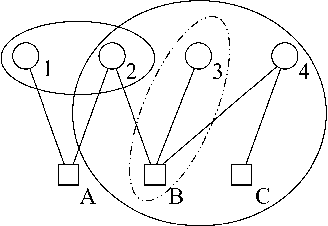
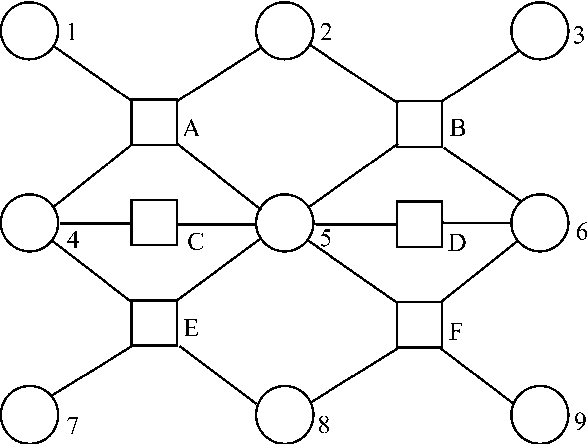
Many large MDPs can be represented compactly using a dynamic Bayesian network. Although the structure of the value function does not retain the structure of the process, recent work has shown that value functions in factored MDPs can often be approximated well using a decomposed value function: a linear combination of <I>restricted</I> basis functions, each of which refers only to a small subset of variables. An approximate value function for a particular policy can be computed using approximate dynamic programming, but this approach (and others) can only produce an approximation relative to a distance metric which is weighted by the stationary distribution of the current policy. This type of weighted projection is ill-suited to policy improvement. We present a new approach to value determination, that uses a simple closed-form computation to directly compute a least-squares decomposed approximation to the value function <I>for any weights</I>. We then use this value determination algorithm as a subroutine in a policy iteration process. We show that, under reasonable restrictions, the policies induced by a factored value function are compactly represented, and can be manipulated efficiently in a policy iteration process. We also present a method for computing error bounds for decomposed value functions using a variable-elimination algorithm for function optimization. The complexity of all of our algorithms depends on the factorization of system dynamics and of the approximate value function.

Inference in Hybrid Networks: Theoretical Limits and Practical Algorithms

An important subclass of hybrid Bayesian networks are those that represent Conditional Linear Gaussian (CLG) distributions --- a distribution with a multivariate Gaussian component for each instantiation of the discrete variables. In this paper we explore the problem of inference in CLGs. We show that inference in CLGs can be significantly harder than inference in Bayes Nets. In particular, we prove that even if the CLG is restricted to an extremely simple structure of a polytree in which every continuous node has at most one discrete ancestor, the inference task is NP-hard.To deal with the often prohibitive computational cost of the exact inference algorithm for CLGs, we explore several approximate inference algorithms. These algorithms try to find a small subset of Gaussians which are a good approximation to the full mixture distribution. We consider two Monte Carlo approaches and a novel approach that enumerates mixture components in order of prior probability. We compare these methods on a variety of problems and show that our novel algorithm is very promising for large, hybrid diagnosis problems.

Value Function Approximation in Zero-Sum Markov Games

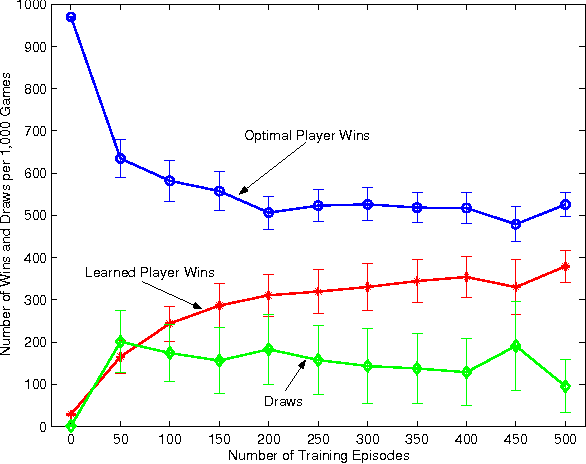
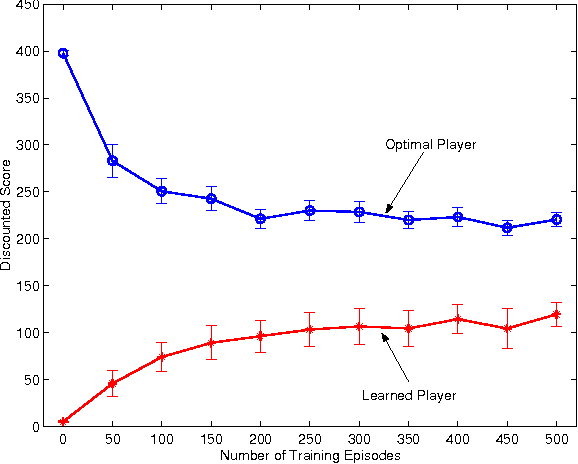
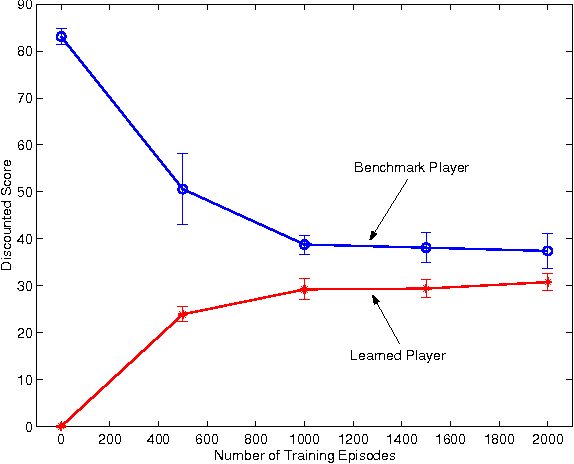
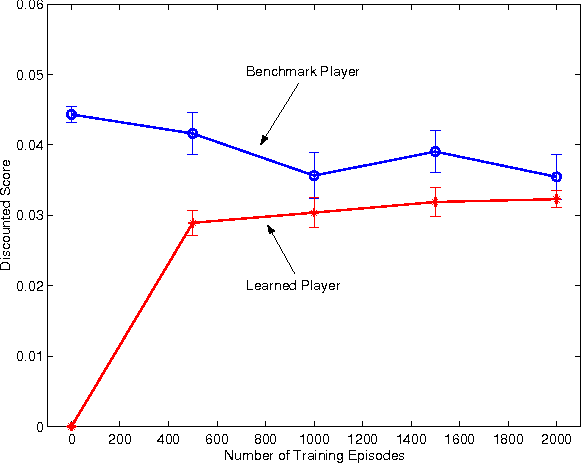
This paper investigates value function approximation in the context of zero-sum Markov games, which can be viewed as a generalization of the Markov decision process (MDP) framework to the two-agent case. We generalize error bounds from MDPs to Markov games and describe generalizations of reinforcement learning algorithms to Markov games. We present a generalization of the optimal stopping problem to a two-player simultaneous move Markov game. For this special problem, we provide stronger bounds and can guarantee convergence for LSTD and temporal difference learning with linear value function approximation. We demonstrate the viability of value function approximation for Markov games by using the Least squares policy iteration (LSPI) algorithm to learn good policies for a soccer domain and a flow control problem.

Value Function Approximation in Noisy Environments Using Locally Smoothed Regularized Approximate Linear Programs

Recently, Petrik et al. demonstrated that L1Regularized Approximate Linear Programming (RALP) could produce value functions and policies which compared favorably to established linear value function approximation techniques like LSPI. RALP's success primarily stems from the ability to solve the feature selection and value function approximation steps simultaneously. RALP's performance guarantees become looser if sampled next states are used. For very noisy domains, RALP requires an accurate model rather than samples, which can be unrealistic in some practical scenarios. In this paper, we demonstrate this weakness, and then introduce Locally Smoothed L1-Regularized Approximate Linear Programming (LS-RALP). We demonstrate that LS-RALP mitigates inaccuracies stemming from noise even without an accurate model. We show that, given some smoothness assumptions, as the number of samples increases, error from noise approaches zero, and provide experimental examples of LS-RALP's success on common reinforcement learning benchmark problems.

Efficient Selection of Disambiguating Actions for Stereo Vision

In many domains that involve the use of sensors, such as robotics or sensor networks, there are opportunities to use some form of active sensing to disambiguate data from noisy or unreliable sensors. These disambiguating actions typically take time and expend energy. One way to choose the next disambiguating action is to select the action with the greatest expected entropy reduction, or information gain. In this work, we consider active sensing in aid of stereo vision for robotics. Stereo vision is a powerful sensing technique for mobile robots, but it can fail in scenes that lack strong texture. In such cases, a structured light source, such as vertical laser line can be used for disambiguation. By treating the stereo matching problem as a specially structured HMM-like graphical model, we demonstrate that for a scan line with n columns and maximum stereo disparity d, the entropy minimizing aim point for the laser can be selected in O(nd) time - cost no greater than the stereo algorithm itself. In contrast, a typical HMM formulation would suggest at least O(nd^2) time for the entropy calculation alone.

Feature Selection Using Regularization in Approximate Linear Programs for Markov Decision Processes

Approximate dynamic programming has been used successfully in a large variety of domains, but it relies on a small set of provided approximation features to calculate solutions reliably. Large and rich sets of features can cause existing algorithms to overfit because of a limited number of samples. We address this shortcoming using $L_1$ regularization in approximate linear programming. Because the proposed method can automatically select the appropriate richness of features, its performance does not degrade with an increasing number of features. These results rely on new and stronger sampling bounds for regularized approximate linear programs. We also propose a computationally efficient homotopy method. The empirical evaluation of the approach shows that the proposed method performs well on simple MDPs and standard benchmark problems.