Policy Iteration for Factored MDPs

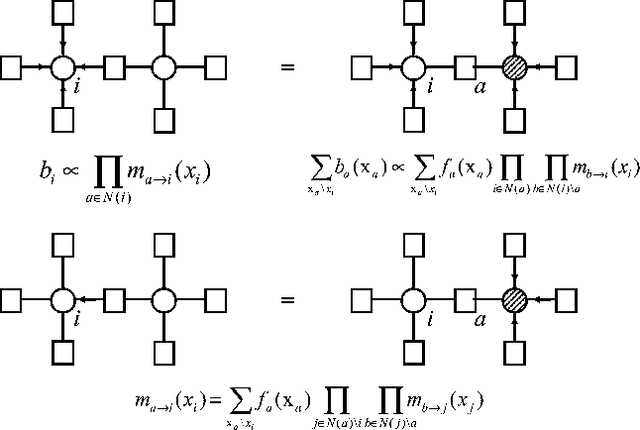
Many large MDPs can be represented compactly using a dynamic Bayesian network. Although the structure of the value function does not retain the structure of the process, recent work has shown that value functions in factored MDPs can often be approximated well using a decomposed value function: a linear combination of <I>restricted</I> basis functions, each of which refers only to a small subset of variables. An approximate value function for a particular policy can be computed using approximate dynamic programming, but this approach (and others) can only produce an approximation relative to a distance metric which is weighted by the stationary distribution of the current policy. This type of weighted projection is ill-suited to policy improvement. We present a new approach to value determination, that uses a simple closed-form computation to directly compute a least-squares decomposed approximation to the value function <I>for any weights</I>. We then use this value determination algorithm as a subroutine in a policy iteration process. We show that, under reasonable restrictions, the policies induced by a factored value function are compactly represented, and can be manipulated efficiently in a policy iteration process. We also present a method for computing error bounds for decomposed value functions using a variable-elimination algorithm for function optimization. The complexity of all of our algorithms depends on the factorization of system dynamics and of the approximate value function.