A General Algorithm for Approximate Inference and its Application to Hybrid Bayes Nets

The clique tree algorithm is the standard method for doing inference in Bayesian networks. It works by manipulating clique potentials - distributions over the variables in a clique. While this approach works well for many networks, it is limited by the need to maintain an exact representation of the clique potentials. This paper presents a new unified approach that combines approximate inference and the clique tree algorithm, thereby circumventing this limitation. Many known approximate inference algorithms can be viewed as instances of this approach. The algorithm essentially does clique tree propagation, using approximate inference to estimate the densities in each clique. In many settings, the computation of the approximate clique potential can be done easily using statistical importance sampling. Iterations are used to gradually improve the quality of the estimation.

Exact Inference in Networks with Discrete Children of Continuous Parents

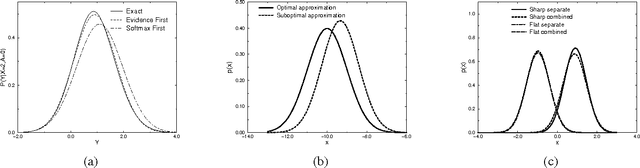
Many real life domains contain a mixture of discrete and continuous variables and can be modeled as hybrid Bayesian Networks. Animportant subclass of hybrid BNs are conditional linear Gaussian (CLG) networks, where the conditional distribution of the continuous variables given an assignment to the discrete variables is a multivariate Gaussian. Lauritzen's extension to the clique tree algorithm can be used for exact inference in CLG networks. However, many domains also include discrete variables that depend on continuous ones, and CLG networks do not allow such dependencies to berepresented. No exact inference algorithm has been proposed for these enhanced CLG networks. In this paper, we generalize Lauritzen's algorithm, providing the first "exact" inference algorithm for augmented CLG networks - networks where continuous nodes are conditional linear Gaussians but that also allow discrete children ofcontinuous parents. Our algorithm is exact in the sense that it computes the exact distributions over the discrete nodes, and the exact first and second moments of the continuous ones, up to the accuracy obtained by numerical integration used within thealgorithm. When the discrete children are modeled with softmax CPDs (as is the case in many real world domains) the approximation of the continuous distributions using the first two moments is particularly accurate. Our algorithm is simple to implement and often comparable in its complexity to Lauritzen's algorithm. We show empirically that it achieves substantially higher accuracy than previous approximate algorithms.

Inference in Hybrid Networks: Theoretical Limits and Practical Algorithms

An important subclass of hybrid Bayesian networks are those that represent Conditional Linear Gaussian (CLG) distributions --- a distribution with a multivariate Gaussian component for each instantiation of the discrete variables. In this paper we explore the problem of inference in CLGs. We show that inference in CLGs can be significantly harder than inference in Bayes Nets. In particular, we prove that even if the CLG is restricted to an extremely simple structure of a polytree in which every continuous node has at most one discrete ancestor, the inference task is NP-hard.To deal with the often prohibitive computational cost of the exact inference algorithm for CLGs, we explore several approximate inference algorithms. These algorithms try to find a small subset of Gaussians which are a good approximation to the full mixture distribution. We consider two Monte Carlo approaches and a novel approach that enumerates mixture components in order of prior probability. We compare these methods on a variety of problems and show that our novel algorithm is very promising for large, hybrid diagnosis problems.

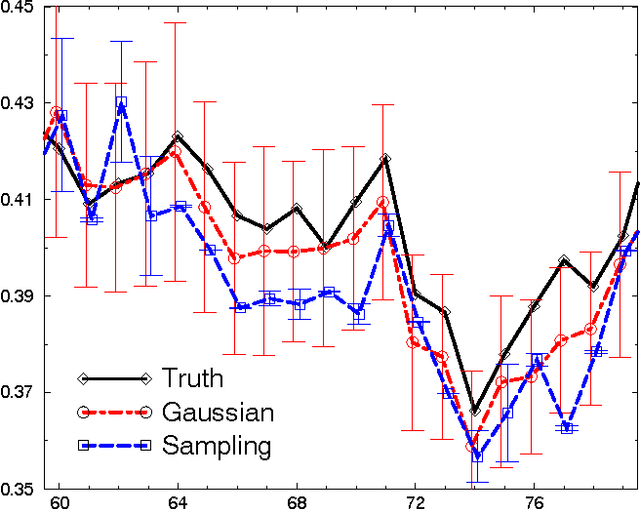
Monitoring a Complez Physical System using a Hybrid Dynamic Bayes Net

The Reverse Water Gas Shift system (RWGS) is a complex physical system designed to produce oxygen from the carbon dioxide atmosphere on Mars. If sent to Mars, it would operate without human supervision, thus requiring a reliable automated system for monitoring and control. The RWGS presents many challenges typical of real-world systems, including: noisy and biased sensors, nonlinear behavior, effects that are manifested over different time granularities, and unobservability of many important quantities. In this paper we model the RWGS using a hybrid (discrete/continuous) Dynamic Bayesian Network (DBN), where the state at each time slice contains 33 discrete and 184 continuous variables. We show how the system state can be tracked using probabilistic inference over the model. We discuss how to deal with the various challenges presented by the RWGS, providing a suite of techniques that are likely to be useful in a wide range of applications. In particular, we describe a general framework for dealing with nonlinear behavior using numerical integration techniques, extending the successful Unscented Filter. We also show how to use a fixed-point computation to deal with effects that develop at different time scales, specifically rapid changes occurring during slowly changing processes. We test our model using real data collected from the RWGS, demonstrating the feasibility of hybrid DBNs for monitoring complex real-world physical systems.