Enhancing Self-Training Methods

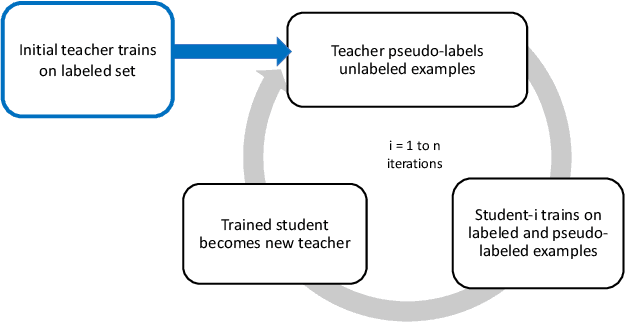
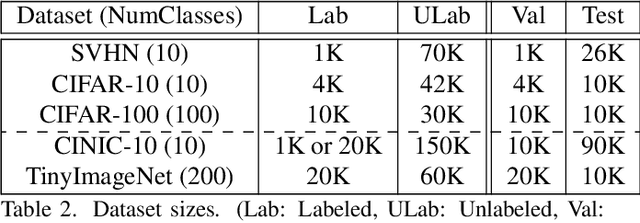
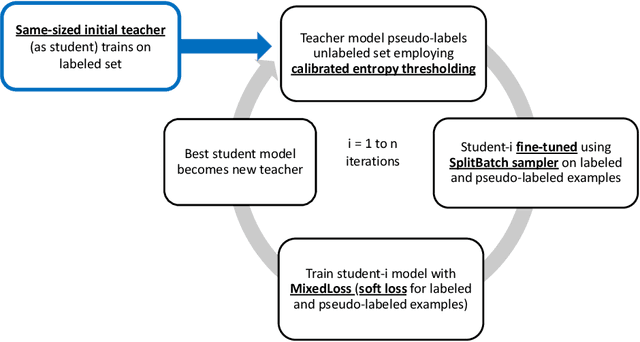
Semi-supervised learning approaches train on small sets of labeled data along with large sets of unlabeled data. Self-training is a semi-supervised teacher-student approach that often suffers from the problem of "confirmation bias" that occurs when the student model repeatedly overfits to incorrect pseudo-labels given by the teacher model for the unlabeled data. This bias impedes improvements in pseudo-label accuracy across self-training iterations, leading to unwanted saturation in model performance after just a few iterations. In this work, we describe multiple enhancements to improve the self-training pipeline to mitigate the effect of confirmation bias. We evaluate our enhancements over multiple datasets showing performance gains over existing self-training design choices. Finally, we also study the extendability of our enhanced approach to Open Set unlabeled data (containing classes not seen in labeled data).

Bottom-up Hierarchical Classification Using Confusion-based Logit Compression

In this work, we propose a method to efficiently compute label posteriors of a base flat classifier in the presence of few validation examples within a bottom-up hierarchical inference framework. A stand-alone validation set (not used to train the base classifier) is preferred for posterior estimation to avoid overfitting the base classifier, however a small validation set limits the number of features one can effectively use. We propose a simple, yet robust, logit vector compression approach based on generalized logits and label confusions for the task of label posterior estimation within the context of hierarchical classification. Extensive comparative experiments with other compression techniques are provided across multiple sized validation sets, and a comparison with related hierarchical classification approaches is also conducted. The proposed approach mitigates the problem of not having enough validation examples for reliable posterior estimation while maintaining strong hierarchical classification performance.

A Classification Refinement Strategy for Semantic Segmentation

Based on the observation that semantic segmentation errors are partially predictable, we propose a compact formulation using confusion statistics of the trained classifier to refine (re-estimate) the initial pixel label hypotheses. The proposed strategy is contingent upon computing the classifier confusion probabilities for a given dataset and estimating a relevant prior on the object classes present in the image to be classified. We provide a procedure to robustly estimate the confusion probabilities and explore multiple prior definitions. Experiments are shown comparing performances on multiple challenging datasets using different priors to improve a state-of-the-art semantic segmentation classifier. This study demonstrates the potential to significantly improve semantic labeling and motivates future work for reliable label prior estimation from images.

Formal Concept Analysis of Rodent Carriers of Zoonotic Disease

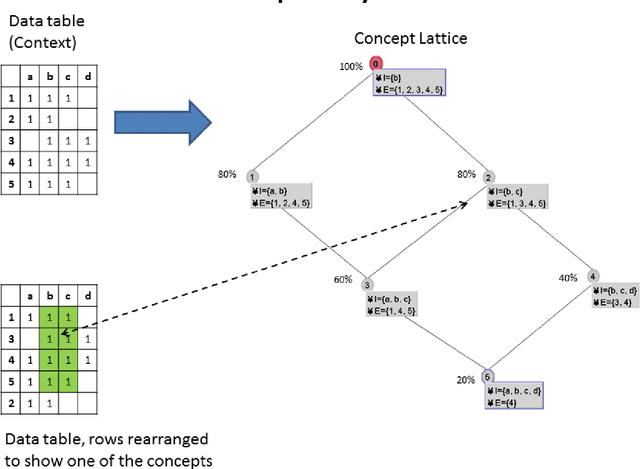
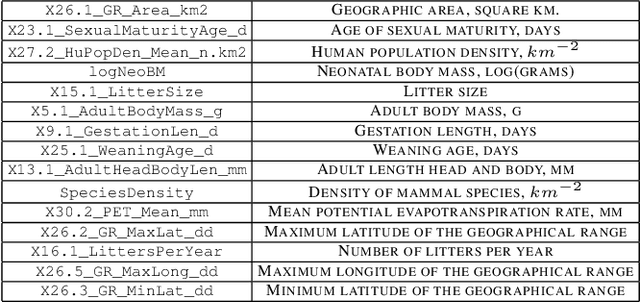
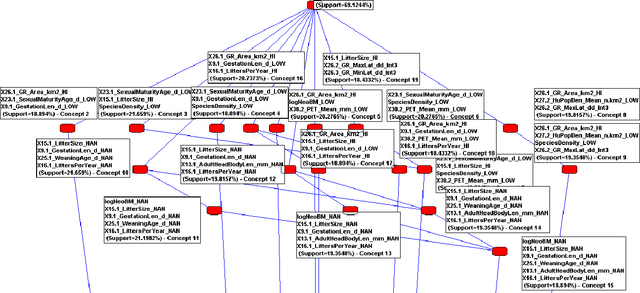
The technique of Formal Concept Analysis is applied to a dataset describing the traits of rodents, with the goal of identifying zoonotic disease carriers,or those species carrying infections that can spillover to cause human disease. The concepts identified among these species together provide rules-of-thumb about the intrinsic biological features of rodents that carry zoonotic diseases, and offer utility for better targeting field surveillance efforts in the search for novel disease carriers in the wild.

Beyond Feedforward Models Trained by Backpropagation: a Practical Training Tool for a More Efficient Universal Approximator

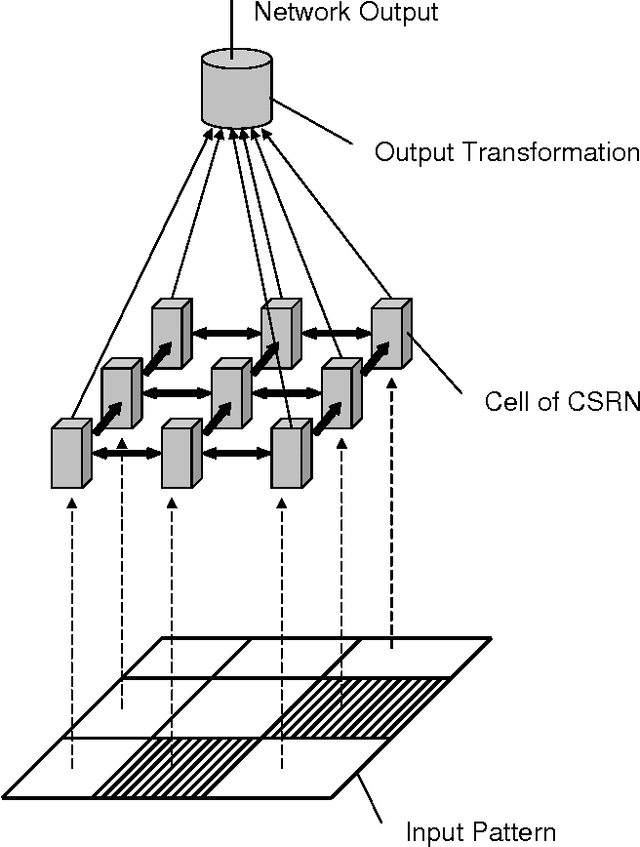
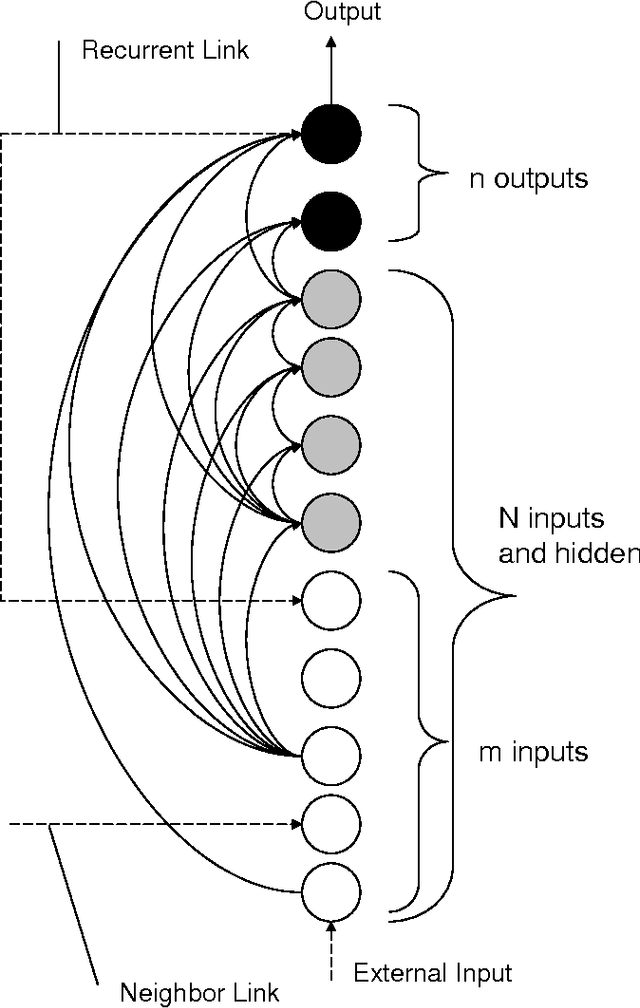
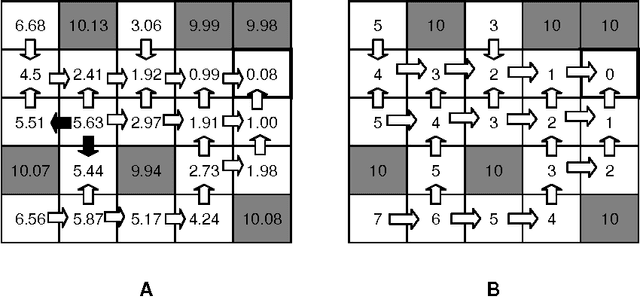
Cellular Simultaneous Recurrent Neural Network (SRN) has been shown to be a function approximator more powerful than the MLP. This means that the complexity of MLP would be prohibitively large for some problems while SRN could realize the desired mapping with acceptable computational constraints. The speed of training of complex recurrent networks is crucial to their successful application. Present work improves the previous results by training the network with extended Kalman filter (EKF). We implemented a generic Cellular SRN and applied it for solving two challenging problems: 2D maze navigation and a subset of the connectedness problem. The speed of convergence has been improved by several orders of magnitude in comparison with the earlier results in the case of maze navigation, and superior generalization has been demonstrated in the case of connectedness. The implications of this improvements are discussed.