Beyond Feedforward Models Trained by Backpropagation: a Practical Training Tool for a More Efficient Universal Approximator
Paper and Code
Oct 23, 2007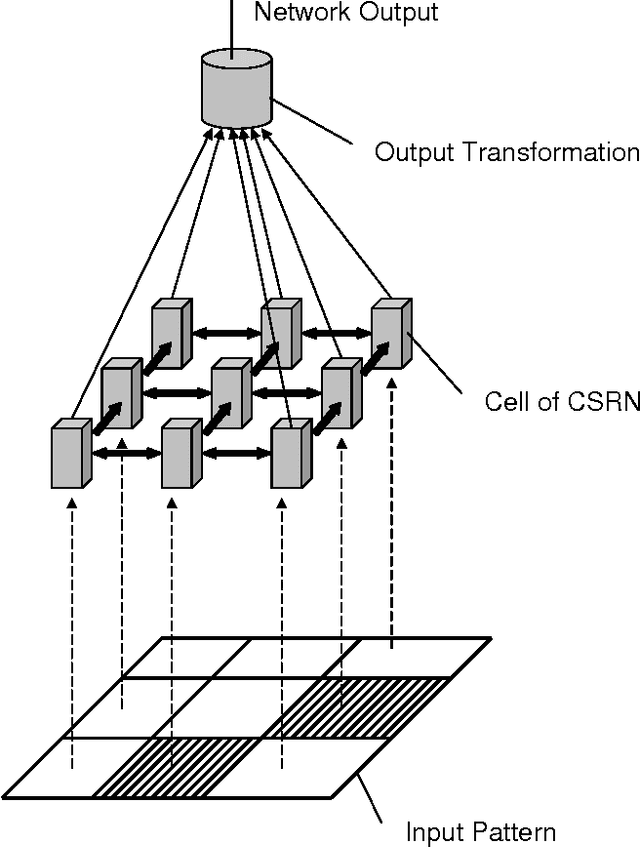
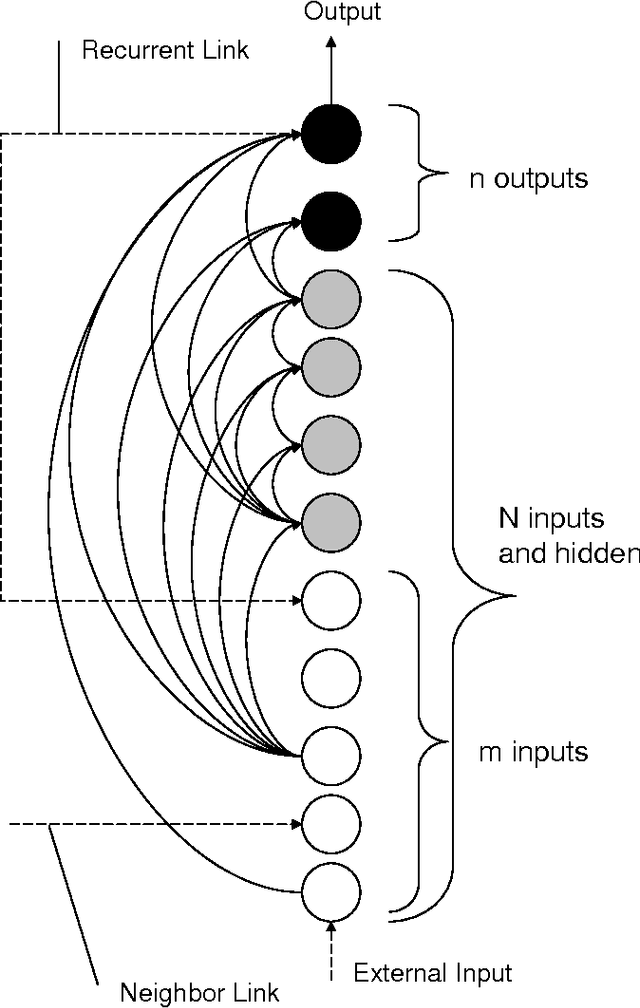

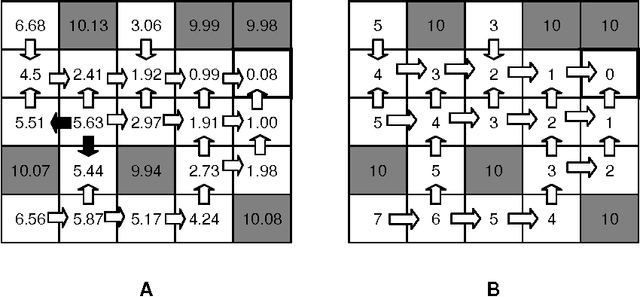
Cellular Simultaneous Recurrent Neural Network (SRN) has been shown to be a function approximator more powerful than the MLP. This means that the complexity of MLP would be prohibitively large for some problems while SRN could realize the desired mapping with acceptable computational constraints. The speed of training of complex recurrent networks is crucial to their successful application. Present work improves the previous results by training the network with extended Kalman filter (EKF). We implemented a generic Cellular SRN and applied it for solving two challenging problems: 2D maze navigation and a subset of the connectedness problem. The speed of convergence has been improved by several orders of magnitude in comparison with the earlier results in the case of maze navigation, and superior generalization has been demonstrated in the case of connectedness. The implications of this improvements are discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge