Complete stability analysis of a heuristic ADP control design

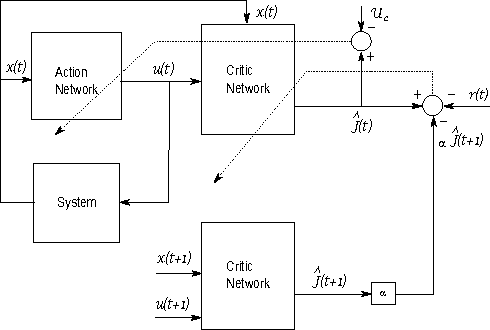
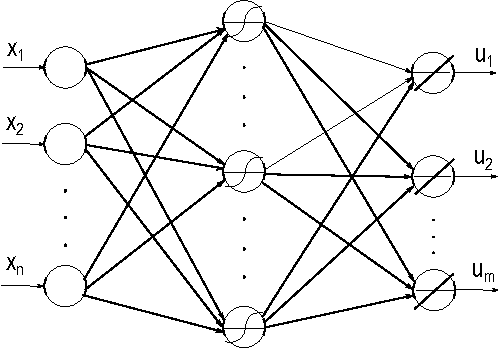
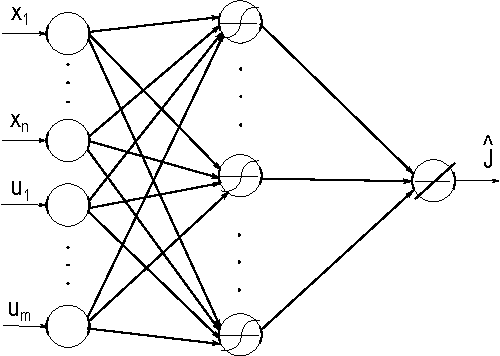
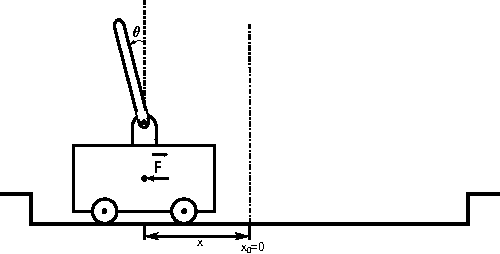
This paper provides new stability results for Action-Dependent Heuristic Dynamic Programming (ADHDP), using a control algorithm that iteratively improves an internal model of the external world in the autonomous system based on its continuous interaction with the environment. We extend previous results by ADHDP control to the case of general multi-layer neural networks with deep learning across all layers. In particular, we show that the introduced control approach is uniformly ultimately bounded (UUB) under specific conditions on the learning rates, without explicit constraints on the temporal discount factor. We demonstrate the benefit of our results to the control of linear and nonlinear systems, including the cart-pole balancing problem. Our results show significantly improved learning and control performance as compared to the state-of-art.

Brain-Like Stochastic Search: A Research Challenge and Funding Opportunity

Brain-Like Stochastic Search (BLiSS) refers to this task: given a family of utility functions U(u,A), where u is a vector of parameters or task descriptors, maximize or minimize U with respect to u, using networks (Option Nets) which input A and learn to generate good options u stochastically. This paper discusses why this is crucial to brain-like intelligence (an area funded by NSF) and to many applications, and discusses various possibilities for network design and training. The appendix discusses recent research, relations to work on stochastic optimization in operations research, and relations to engineering-based approaches to understanding neocortex.

Beyond Feedforward Models Trained by Backpropagation: a Practical Training Tool for a More Efficient Universal Approximator

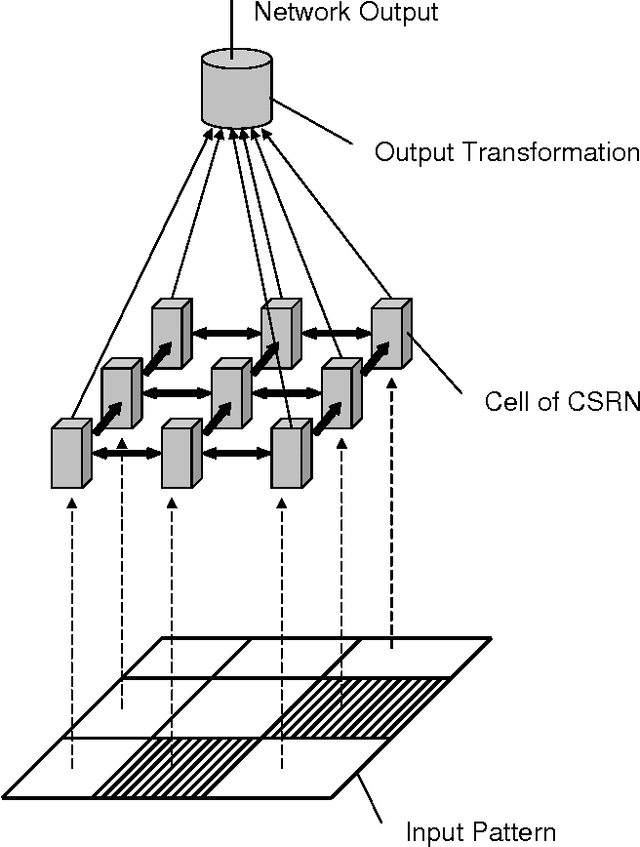
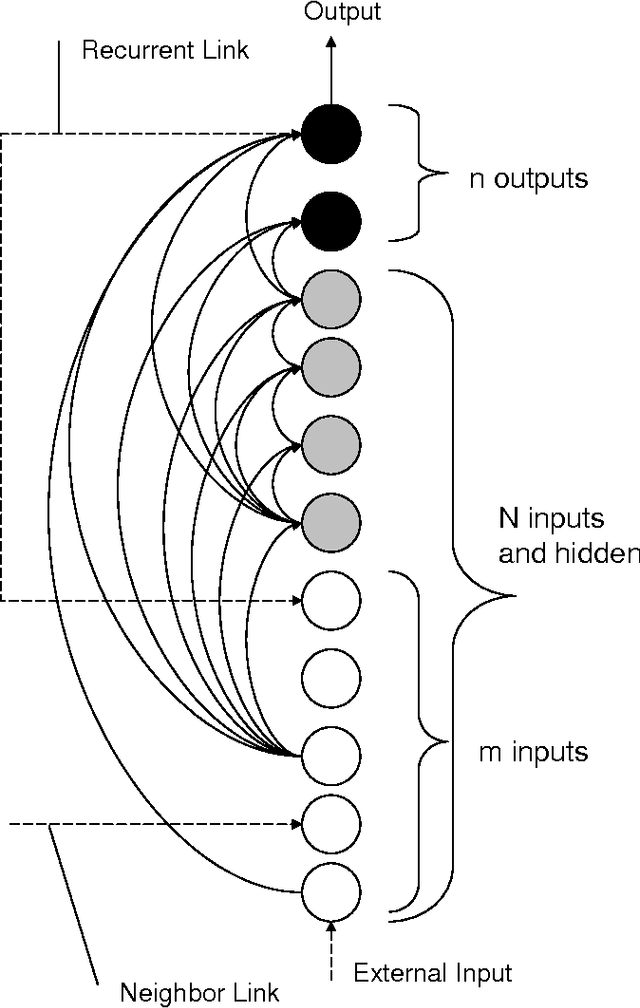
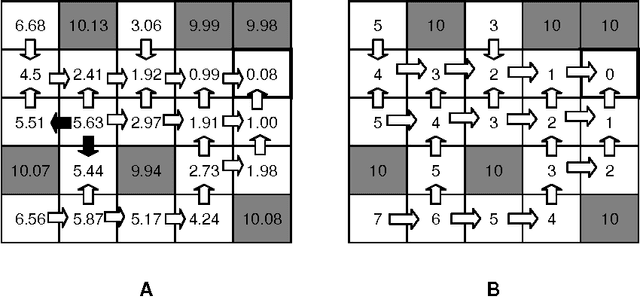
Cellular Simultaneous Recurrent Neural Network (SRN) has been shown to be a function approximator more powerful than the MLP. This means that the complexity of MLP would be prohibitively large for some problems while SRN could realize the desired mapping with acceptable computational constraints. The speed of training of complex recurrent networks is crucial to their successful application. Present work improves the previous results by training the network with extended Kalman filter (EKF). We implemented a generic Cellular SRN and applied it for solving two challenging problems: 2D maze navigation and a subset of the connectedness problem. The speed of convergence has been improved by several orders of magnitude in comparison with the earlier results in the case of maze navigation, and superior generalization has been demonstrated in the case of connectedness. The implications of this improvements are discussed.